神经网络语言模型

 NLP   |  2021年10月10日   |  阅读：2962次

1. 语言模型

什么是语言模型？通俗的来讲是判断一句话是否符合人说话的模型，如可以说”猫有四条腿“，却不能说”四条腿有猫“。因为”四条腿有猫“这样的表述不符合人们的正常语言规范。在语言模型的发展过程中，分别出现了专家语法规则模型，统计语言模型，神经网络语言模型三个阶段。其中，专家语法规则模型出现在语言模型的初始阶段，我们知道，每一种语言都有其特定的语法规则，因此在早期，人们设法通过归纳出的语法规则来对语言建模；统计语言模型则是对句子的概率分布建模，通过对大量语料的统计发现，符合人们正常语言规范的句子出现的概率要大于不符合语言规范的句子，如上述的“猫有四条腿”出现的概率要大于“四条腿有猫”的概率；神经网络语言模型是在统计语言模型的基础上，通过神经网络模型对句子的概率分布建模的方法。下面将从统计语言模型开始讲起。

2. 统计语言模型

2.1. 统计语言模型

统计语言模型（statistical language modeling）通过对大量语料的统计预测出句子的分布。用形式表述，即对于一段文本序列S=w1,w2,⋯ ,wTS=w_1,w_2,\cdots ,w_T，它的概率可以表示为

P(S)=P(w1,w2,⋯ ,wT)P\left ( S \right )=P\left ( w_1,w_2,\cdots ,w_T \right )

通过概率中的链式法则，可以求得上述句子的概率值：

P(w1,w2,⋯ ,wT)=P(w1)⋅P(w2∣w1)⋯P(wT∣w1,w2,⋯wT−1)P\left ( w_1,w_2,\cdots ,w_T \right )=P\left ( w_1 \right )\cdot P\left ( w_2\mid w_1 \right )\cdots P\left ( w_T\mid w_1,w_2,\cdots w_{T-1} \right )

其中，P(wi∣w1,⋯ ,wi−1)P\left ( w_i\mid w_1,\cdots ,w_{i-1} \right )表示的是在词w1,⋯ ,wi−1w_1,\cdots ,w_{i-1}出现的条件下词wiw_i出现的概率，对于以上的统计语言模型，每一个词的概率便是模型的参数，如上述的P(w1)P\left ( w_1 \right )，P(w2∣w1)P\left ( w_2\mid w_1 \right )等。为了计算模型的参数，需要统计每个词出现的概率，如对于词wiw_i，可以通过以下的方式统计得到：

P(wi∣w1,⋯ ,wi−1)=N(w1,w2,⋯ ,wi)N(w1,w2,⋯ ,wi−1)P\left ( w_i\mid w_1,\cdots ,w_{i-1} \right )=\frac{N_{\left ( w_1,w_2,\cdots ,w_i \right )}}{N_{\left ( w_1,w_2,\cdots ,w_{i-1} \right )}}

其中，N(w1,w2,⋯ ,wi)N_{\left ( w_1,w_2,\cdots ,w_i \right )}表示的在文本语料中出现文本序列w1,w2,⋯ ,wiw_1,w_2,\cdots ,w_i的次数。

在实际的过程中，如果文本的长度比较长，要估算P(wi∣w1,⋯ ,wi−1)P\left ( w_i\mid w_1,\cdots ,w_{i-1} \right )是非常困难的，主要体现在以下的两个方面：

  1. 需要计算的参数过多。假设词库VV的大小为100000，对于包含10个词的序列，潜在的参数个数为10000010−1100000^{10}-1；
  2. 数据极度稀疏，长序列的出现频次较低；

2.2. n-gram模型

为了简化上述的问题，通常在估算条件概率时，距离大于等于nn的上文词会被忽略，即所谓的n-gram模型。n-gram模型是基于马尔科夫假设，即当前词出现的概率仅依赖前n−1n−1个词

P(wi∣w1,⋯ ,wi−1)≈P(wi∣wi−n+1,⋯ ,wi−1)P\left ( w_i\mid w_1,\cdots ,w_{i-1} \right )\approx P\left ( w_i\mid w_{i−n+1},\cdots ,w_{i-1} \right )

当n=1n=1时，又称为unigram（一元语言模型），句子的概率值为P(w1,w2,⋯ ,wT)=P(w1)⋅P(w2)⋯P(wT)P\left ( w_1,w_2,\cdots ,w_T \right )=P\left ( w_1 \right )\cdot P\left ( w_2 \right )\cdots P\left ( w_T \right )，从公式可以看出，u nigram模型中，句子的概率为其中的每个词的概率的乘积，即假设每个词是相互独立的，这样句子中的词序信息会丢失，虽然估算方便了，但是效果会有较大的损耗；为了解决性能和效率的问题，通常设置n=2n=2或者n=3n=3，当n=2n=2时，又称为bigram（二元语言模型），当n=3n=3时，又称为trigram（三元语言模型），即当前词部分依赖上文中的词。

3. 神经网络语言模型

在n-gram模型中，为了更好地保留词序信息，构建更强大的语言模型，通常希望选择较大的nn。当nn较大时，长度为nn的序列出现的次数就会非常少，数据稀疏的问题依然没有能够解决。为了更好地解决n-gram中估算概率遇到的数据稀疏问题，神经网络语言模型应运而生。NNLM（Nerual Network Language Model）是经典的用神经语言模型，在论文《A Neural Probabilistic Language Model》中提出。

3.1. NNLM原理

对于神经网络语言模型，训练数据集与上述一致，是一系列词的集合构成的序列：S=w1,w2,⋯ ,wTS=w_1,w_2,\cdots ,w_T，其中，wt∈Vw_t\in V，VV表示的是词库。NNLM的目标函数为：

f(wt,⋯ ,wt−n+1)=P(wt∣w1,⋯ ,wt−1)f\left ( w_t,\cdots ,w_{t-n+1} \right )=P\left ( w_t\mid w_1,\cdots ,w_{t-1} \right )

神经网络语言模型通过词wtw_t的前n−1n-1个词wt−n+1,⋯ ,wt−1w_{t-n+1},\cdots ,w_{t-1}估算出概率P(wt∣w1,⋯ ,wt−1)P\left ( w_t\mid w_1,\cdots ,w_{t-1} \right )，从而避免大量的统计工作。这里有两个限制条件：

  1. ∑i=1∣V∣f(i,wt−1,⋯ ,wt−n+1)=1\sum_{i=1}^{\left | V \right |}f\left ( i,w_{t-1},\cdots ,w_{t-n+1} \right )=1
  2. f>0

神经语言模型NNLM采用普通的三层前馈神经网络结构，其网络结构如下图所示（与通常的三层前馈神经网络略有不同）：

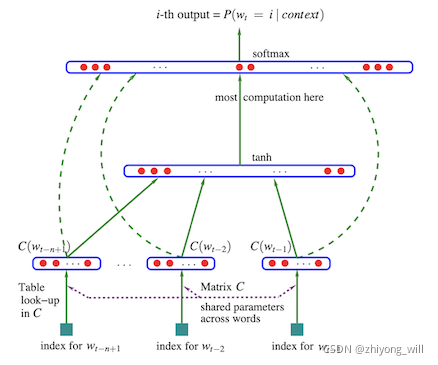
在这里插入图片描述

从网络结构可以看出，三层的网络中第一层为输入层，通过一个映射矩阵CC（CC可以认为是一个∣V∣×m\left | V \right |\times m的共享矩阵，将词库VV中的每个词映射成对应的向量，可通过索引的方式取得对应词的词向量）将前nn个词映射成mm维的词向量，如词库VV中的第ii个词，映射成词向量后为C(i)∈RmC\left ( i \right )\in\mathbb{R}^m，生成前n−1n-1个词的向量表示xx：

x=(C(wt−1),C(wt−2),⋯ ,C(wt−n+1))x=\left ( C\left ( w_{t-1} \right ),C\left ( w_{t-2} \right ),\cdots ,C\left ( w_{t-n+1} \right ) \right )

当输入层完成对上文的n−1n-1个词的词向量表示后，模型将数据送入到剩下的两层网络中，分别为隐藏层和输出层yy：

y=b+Wx+Utanh(d+Hx)y=b+Wx+Utanh\left ( d+Hx \right )

假设hh表示隐藏层的神经元个数，那么H∈Rh×(n−1)mH\in \mathbb{R}^{h\times \left ( n-1 \right )m}，d∈Rhd\in \mathbb{R}^{h}，U∈R∣V∣×hU\in \mathbb{R}^{\left | V \right |\times h}，W∈R∣V∣×(n−1)mW\in \mathbb{R}^{\left | V \right |\times \left ( n-1 \right )m}，b∈R∣V∣b\in \mathbb{R}^{\left | V \right |}。

输出层共有∣V∣\left | V \right |个神经元，依次对应着词库VV中每个词的可能性。为了使得所有神经元的结果之和为11，在输出层yy之后，需要加入softmax函数，将yy专程对应的概率值：

P(wt∣wt−n+1,⋯ ,wt−1)=exp(ywt)∑iexp(yi)P\left ( w_t\mid w_{t−n+1},\cdots ,w_{t-1} \right )=\frac{exp\left ( y_{w_t} \right )}{\sum _iexp\left ( y_i \right )}

3.2. 模型训练

综上，模型中的参数为θ=(b,d,W,U,H,C)\theta =\left ( b,d,W,U,H,C \right )，对于整个语料，神经网络语言模型需要最大化：

L=1T∑tlog f(wt,wt−1,⋯ ,wt−n+1;θ)+R(θ)L=\frac{1}{T}\sum _tlog\: f\left ( w_t,w_{t-1},\cdots ,w_{t-n+1}; \theta \right )+R\left ( \theta \right )

其中R(θ)R\left ( \theta \right )为正则项，对于神经网络的训练，通常使用梯度下降对损失函数求解，对于上述的最大化问题，可通过下述公式迭代求解：

θ←θ+ϵ∂L∂θ\theta \leftarrow \theta +\epsilon \frac{\partial L}{\partial \theta }

参考文献

[1] Kandola E J , Hofmann T , Poggio T , et al. A Neural Probabilistic Language Model[J]. Studies in Fuzziness & Soft Computing, 2006, 194:137-186.

目录