1. 概述 PNN(Product-based Neural Network)是在2016年提出的用于计算CTR问题的深度神经网络模型,PNN的网络结构对传统的FNN(Feedforward Neural Network)网络结构做了一些优化,使得其能够更适合处理CTR问题。在PNN网络模型中,主要的优化点为:
通过Embedding层处理离散特征。Embedding层现在已经成为DNN模型处理CTR问题的标配;
增加Product层,在Product Layer中,通过显式构造特征交叉,在不同的特征域之间进行特征组合,在实际的实施过程中,会有不同的product计算方法,在参考文献[1]中,提到了两种不同的product计算方法,分别为inner producr和outer product。
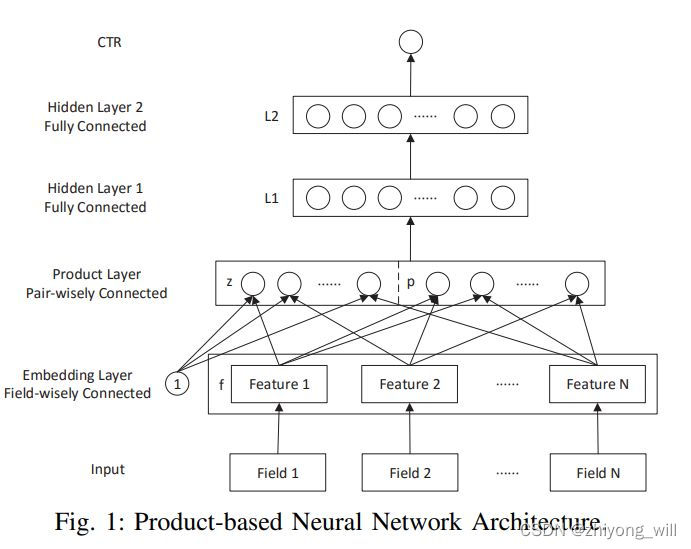
2. 算法原理 2.1. PNN的网络结构 PNN的网络结构如下图所示:
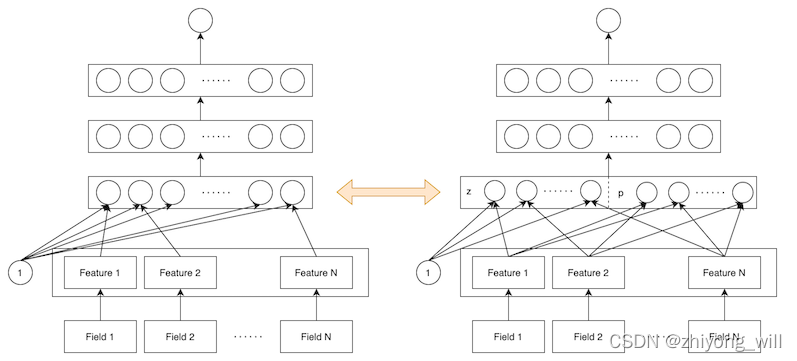
从网络结构上看,整个网络分成四层,第一层为特征Embedding层,第二层为Product层(PNN最为核心的部分), 第三层与第四层是传统的全连接网络层,最后模型的输出层。其网络结构与传统的DNN网络结构基本一致,不同的就是比传统DNN网络结构增加了Product层,与传统DNN的网络结构对比如下图所示:
2.2. PNN网络的计算过程 从上到下最上层上PNN的输出层,PNN网络的输出为
y ^ = σ ( W 3 l 2 + b 3 ) \hat{y}=\sigma \left (\mathbf{W}_3\mathbf{l}_2+b_3\right ) y ^ = σ ( W 3 l 2 + b 3 )
其中,W 3 ∈ R 1 × D 2 \mathbf{W}_3\in \mathbb{R}^{1\times D_2} W 3 ∈ R 1 × D 2 b 3 ∈ R b_3\in \mathbb{R} b 3 ∈ R l 2 ∈ R D 2 \mathbf{l}_2\in \mathbb{R}^{D_2} l 2 ∈ R D 2 D 2 D_2 D 2 σ \sigma σ l 2 \mathbf{l}_2 l 2
l 2 = r e l u ( W 2 l 1 + b 2 ) \mathbf{l}_2=relu\left ( \mathbf{W}_2\mathbf{l}_1+\mathbf{b}_2 \right ) l 2 = re l u ( W 2 l 1 + b 2 )
其中,W 2 ∈ R D 2 × D 1 \mathbf{W}_2\in \mathbb{R}^{D_2\times D_1} W 2 ∈ R D 2 × D 1 b 2 ∈ R D 2 \mathbf{b}_2\in \mathbb{R}^{D_2} b 2 ∈ R D 2 l 1 ∈ R D 1 \mathbf{l}_1\in \mathbb{R}^{D_1} l 1 ∈ R D 1 D 1 D_1 D 1 r e l u relu re l u l 1 \mathbf{l}_1 l 1
l 1 = r e l u ( l z + l p + b 1 ) \mathbf{l}_1=relu\left ( \mathbf{l}_z+\mathbf{l}_p+\mathbf{b}_1 \right ) l 1 = re l u ( l z + l p + b 1 )
其中,b 1 ∈ R D 1 \mathbf{b}_1\in \mathbb{R}^{D_1} b 1 ∈ R D 1 l z ∈ R D 1 \mathbf{l}_z\in \mathbb{R}^{D_1} l z ∈ R D 1 l p ∈ R D 1 \mathbf{l}_p\in \mathbb{R}^{D_1} l p ∈ R D 1 l z \mathbf{l}_z l z l p \mathbf{l}_p l p
l z = ( l z 1 , l z 2 , ⋯ , l z n , ⋯ , l z D 1 ) , l z n = W z n ⊙ z \mathbf{l}_z=\left ( l_z^1,l_z^2,\cdots ,l_z^n,\cdots ,l_z^{D_1} \right ),\; l_z^n=\mathbf{W}_z^n\odot \mathbf{z} l z = ( l z 1 , l z 2 , ⋯ , l z n , ⋯ , l z D 1 ) , l z n = W z n ⊙ z
l p = ( l p 1 , l p 2 , ⋯ , l p n , ⋯ , l p D 1 ) , l p n = W p n ⊙ p \mathbf{l}_p=\left ( l_p^1,l_p^2,\cdots ,l_p^n,\cdots ,l_p^{D_1} \right ),\; l_p^n=\mathbf{W}_p^n\odot \mathbf{p} l p = ( l p 1 , l p 2 , ⋯ , l p n , ⋯ , l p D 1 ) , l p n = W p n ⊙ p
其中,W z n \mathbf{W}_z^n W z n W p n \mathbf{W}_p^n W p n z \mathbf{z} z p \mathbf{p} p z \mathbf{z} z
z = ( z 1 , z 2 , ⋯ , z N ) = △ ( f 1 , f 2 , ⋯ , f N ) \mathbf{z}=\left ( \mathbf{z}_1,\mathbf{z}_2,\cdots ,\mathbf{z}_N \right )\overset{\underset{\triangle }{}}{=}\left ( \mathbf{f}_1,\mathbf{f}_2,\cdots ,\mathbf{f}_N\right ) z = ( z 1 , z 2 , ⋯ , z N ) = △ ( f 1 , f 2 , ⋯ , f N )
其中,f i ∈ R M \mathbf{f}_i\in \mathbb{R}^M f i ∈ R M i i i p \mathbf{p} p
p = { p i , j } , i = 1 ⋯ N , j = 1 ⋯ N \mathbf{p}=\left\{\mathbf{p}_{i,j} \right\}, i=1\cdots N,j=1\cdots N p = { p i , j } , i = 1 ⋯ N , j = 1 ⋯ N
其中,p i , j = g ( f i , f j ) \mathbf{p}_{i,j}=g\left ( \mathbf{f}_i,\mathbf{f}_j \right ) p i , j = g ( f i , f j ) g g g f i \mathbf{f}_i f i
f i = W 0 i x i [ s t a r t i : e n d i ] \mathbf{f}_i=\mathbf{W}_0^i\: \mathbf{x}_i\left [ start_{i} : end_{i} \right ] f i = W 0 i x i [ s t a r t i : e n d i ]
而对于Product层的函数g g g
2.2.1. Inner Product 在Inner Product中,函数g g g
g ( f i , f j ) = ⟨ f i , f j ⟩ g\left ( \mathbf{f}_i,\mathbf{f}_j \right )=\left \langle \mathbf{f}_i,\mathbf{f}_j \right \rangle g ( f i , f j ) = ⟨ f i , f j ⟩
其中,< f i , f j > \left<\mathbf{f}_i,\mathbf{f}_j \right> ⟨ f i , f j ⟩ f i \mathbf{f}_i f i f j \mathbf{f}_j f j l z n l_z^n l z n l p n l_p^n l p n
l z n = W z n ⊙ z = ∑ i = 1 N ( W z ) i z i = ∑ i = 1 N ( W z ) i f i l_z^n=\mathbf{W}_z^n\odot \mathbf{z}=\sum_{i=1}^{N}\left ( \mathbf{W}_z \right )_{i}\mathbf{z}_i=\sum_{i=1}^{N}\left ( \mathbf{W}_z \right )_{i}\mathbf{f}_i l z n = W z n ⊙ z = i = 1 ∑ N ( W z ) i z i = i = 1 ∑ N ( W z ) i f i
l p n = W p n ⊙ p = ∑ i = 1 N ∑ j = 1 N ( W p n ) i , j p i , j = ∑ i = 1 N ∑ j = 1 N ( W p n ) i , j < f i , f j > l_p^n=\mathbf{W}_p^n\odot \mathbf{p}=\sum_{i=1}^{N}\sum_{j=1}^{N}\left ( \mathbf{W}_p^n \right )_{i,j}\mathbf{p}_{i,j}=\sum_{i=1}^{N}\sum_{j=1}^{N}\left ( \mathbf{W}_p^n \right )_{i,j}\left<\mathbf{f}_i,\mathbf{f}_j \right> l p n = W p n ⊙ p = i = 1 ∑ N j = 1 ∑ N ( W p n ) i , j p i , j = i = 1 ∑ N j = 1 ∑ N ( W p n ) i , j ⟨ f i , f j ⟩
如何去分析Product层的计算复杂度?已知,f i ∈ R M \mathbf{f}_i\in \mathbb{R}^M f i ∈ R M N N N l z n l_z^n l z n O ( N M ) O\left ( NM \right ) O ( NM ) l p n l_p^n l p n O ( N 2 M ) O\left ( N^2M \right ) O ( N 2 M ) l p n l_p^n l p n l p \mathbf{l}_p l p O ( N 2 D 1 ) O\left ( N^2D_1 \right ) O ( N 2 D 1 ) l z \mathbf{l}_z l z O ( D 1 N M ) O\left ( D_1NM \right ) O ( D 1 NM ) l p \mathbf{l}_p l p O ( N 2 ( M + D 1 ) ) O\left ( N^2\left ( M+D_1 \right ) \right ) O ( N 2 ( M + D 1 ) )
受FM算法中参数矩阵分解的启发,参考文献[1]中提出使用矩阵分解的方式来降低时间复杂度。其中要注意p i , j \mathbf{p}_{i,j} p i , j W p n \mathbf{W}_p^n W p n W p n = θ n θ n T \mathbf{W}_p^n=\mathbf{\theta }^n\mathbf{\theta }^{nT} W p n = θ n θ n T θ n ∈ R N \mathbf{\theta }^n\in \mathbb{R}^N θ n ∈ R N l p n l_p^n l p n
l p n = W p n ⊙ p = ∑ i = 1 N ∑ j = 1 N ( W p n ) i , j < f i , f j > = ∑ i = 1 N ∑ j = 1 N θ i n θ j n < f i , f j > = ∑ i = 1 N ∑ j = 1 N < θ i n f i , θ j n f j > = < ∑ i = 1 N θ i n f i , ∑ j = 1 N θ j n f j > = ∥ ∑ i = 1 N δ i n ∥ 2 \begin{aligned}
l_p^n&=\mathbf{W}_p^n\odot \mathbf{p}=\sum_{i=1}^{N}\sum_{j=1}^{N}\left ( \mathbf{W}_p^n \right )_{i,j}\left<\mathbf{f}_i,\mathbf{f}_j \right> \\
&=\sum_{i=1}^{N}\sum_{j=1}^{N}\theta _i^n\theta _j^n\left<\mathbf{f}_i,\mathbf{f}_j \right> \\
&=\sum_{i=1}^{N}\sum_{j=1}^{N}\left<\theta _i^n\mathbf{f}_i,\theta _j^n\mathbf{f}_j \right> \\
&=\left<\sum_{i=1}^{N}\theta _i^n\mathbf{f}_i,\sum_{j=1}^{N}\theta _j^n\mathbf{f}_j \right> \\
&= \left\| \sum_{i=1}^{N}\delta _i^n\right\|^2
\end{aligned} l p n = W p n ⊙ p = i = 1 ∑ N j = 1 ∑ N ( W p n ) i , j ⟨ f i , f j ⟩ = i = 1 ∑ N j = 1 ∑ N θ i n θ j n ⟨ f i , f j ⟩ = i = 1 ∑ N j = 1 ∑ N ⟨ θ i n f i , θ j n f j ⟩ = ⟨ i = 1 ∑ N θ i n f i , j = 1 ∑ N θ j n f j ⟩ = i = 1 ∑ N δ i n 2
其中,δ i n = θ i n f i \delta _i^n=\theta _i^n\mathbf{f}_i δ i n = θ i n f i l p \mathbf{l}_p l p
l p = ( ∥ ∑ i = 1 N δ i 1 ∥ 2 , ⋯ , ∥ ∑ i = 1 N δ i n ∥ 2 , ⋯ , ∥ ∑ i = 1 N δ i D 1 ∥ 2 ) \mathbf{l}_p=\left ( \left\| \sum_{i=1}^{N}\delta _i^1\right\|^2,\cdots ,\left\| \sum_{i=1}^{N}\delta _i^n\right\|^2,\cdots ,\left\| \sum_{i=1}^{N}\delta _i^{D_1}\right\|^2 \right ) l p = i = 1 ∑ N δ i 1 2 , ⋯ , i = 1 ∑ N δ i n 2 , ⋯ , i = 1 ∑ N δ i D 1 2
时间复杂度为O ( D 1 N M ) O\left ( D_1NM \right ) O ( D 1 NM )
2.2.2. Outer Product 在Outer Product中,函数g g g
g ( f i , f j ) = f i f j T g\left ( \mathbf{f}_i,\mathbf{f}_j \right )=\mathbf{f}_i\mathbf{f}_j^T g ( f i , f j ) = f i f j T
此时,由于f i ∈ R M \mathbf{f}_i\in \mathbb{R}^M f i ∈ R M p i , j ∈ R M × M \mathbf{p}_{i,j}\in \mathbb{R}^{M\times M} p i , j ∈ R M × M l p n l_p^n l p n
l p n = W p n ⊙ p = ∑ i = 1 N ∑ j = 1 N ( W p n ) i , j p i , j = ∑ i = 1 N ∑ j = 1 N ( W p n ) i , j f i f j T l_p^n=\mathbf{W}_p^n\odot \mathbf{p}=\sum_{i=1}^{N}\sum_{j=1}^{N}\left ( \mathbf{W}_p^n \right )_{i,j}p_{i,j}=\sum_{i=1}^{N}\sum_{j=1}^{N}\left ( \mathbf{W}_p^n \right )_{i,j}\mathbf{f}_i\mathbf{f}_j^T l p n = W p n ⊙ p = i = 1 ∑ N j = 1 ∑ N ( W p n ) i , j p i , j = i = 1 ∑ N j = 1 ∑ N ( W p n ) i , j f i f j T
对于Outer Product,此时的p i , j \mathbf{p}_{i,j} p i , j M × M M \times M M × M p \mathbf{p} p N × N × M × M N \times N \times M \times M N × N × M × M p \mathbf{p} p O ( M 2 N 2 ) O\left ( M^2N^2 \right ) O ( M 2 N 2 ) l p \mathbf{l}_p l p O ( D 1 M 2 N 2 ) O\left ( D_1M^2N^2 \right ) O ( D 1 M 2 N 2 ) p \mathbf{p} p
p = ∑ i = 1 N ∑ j = 1 N f i f j T = f ∑ ( f ∑ ) T , f ∑ = ∑ i = 1 N f i \mathbf{p}=\sum_{i=1}^{N}\sum_{j=1}^{N}\mathbf{f}_i\mathbf{f}_j^T=\mathbf{f}_{\sum }\left ( \mathbf{f}_{\sum } \right )^T,\; \mathbf{f}_{\sum }=\sum_{i=1}^{N}\mathbf{f}_i p = i = 1 ∑ N j = 1 ∑ N f i f j T = f ∑ ( f ∑ ) T , f ∑ = i = 1 ∑ N f i
此时, p ∈ R M × M \mathbf{p}\in \mathbb{R}^{M\times M} p ∈ R M × M l p \mathbf{l}_p l p O ( D 1 M ( M + N ) ) O\left ( D_1M\left ( M+N \right ) \right ) O ( D 1 M ( M + N ) )
3. 总结 PNN网络结构在传统的DNN中增加了Product层,从而实现了特征的交叉,在具体的实现过程中,提出了两种Product的计算,分别为Inner Product和Outer Product。在具体的数据中,两种Product的表现并不一致,需要根据具体的数据选择合适的Product计算方法,相比较传统的DNN,从实验结果来看,效果上PNN得到了较大提升。
参考文献 [1] Qu Y , Han C , Kan R , et al. Product-Based Neural Networks for User Response Prediction[C]// 2016 IEEE 16th International Conference on Data Mining (ICDM). IEEE, 2016.