1. 概述
Deep&Cross Network(DCN)[1]是由Google于2017年提出的用于计算CTR问题的方法,是对Wide&Deep[2]模型的进一步改进。线性模型无法学习到特征的交叉属性,需要大量的人工特征工程的介入,深度网络对于交叉特征的学习有着天然的优势,在Wide&Deep模型中,Deep侧已经是一个DNN模型,而Wide侧是一个线性模型LR,无法有效的学习到交叉特征。在DCN中针对Wide&Deep模型的Wide侧提出了Cross网络,通过Cross网络学习到更多的交叉特征,提升整个模型的特征表达能力。
2. 算法原理
2.1. DCN的网络结构
DCN模型的网络结构如下图所示:

在DCN网络中,由下到上主要包括五种类型的层,第一种是Embedding层,第二种是Stacking层,用于组合Embedding层的输出;第三种是Cross network的层,用于对Stacking后的特征进行学习;第四种是Deep network的层,作用与Cross network的层一样,此外,Cross network的层和Deep network的层是并行的两个过程;第五种是输出层,经过Cross network的层和Deep network的层后,组合两者的输出做最后的计算。
2.2. DCN网络的计算过程
2.2.1. Embedding和Stacking
对于CTR问题的输入,通常是由一些离散的特征和连续的特征组成,对于离散的特征的处理方法通常是利用one-hot编码对其离散化处理,但是处理后的特征通常是较为稀疏的,举例来说,如类别特征“country=USA”,假设通过one-hot编码后得到的特征为[0,1,0]。这样的特征不适合DNN处理,通常需要通过Embedding将其转换成连续的向量表示,这便是Embedding层的作用,最终得到的Embedding层的输出为:
xembed,i=Wembed,ixi
其中,xembed,i是Embedding层的输出向量,xi是属入的第i个离散特征,Wembed,i∈Rne×nv是一个ne×nv的矩阵,是用于连接输入层到Embedding层的参数。通过Embedding层后,在Stacking层,需要将Embedding层的输出组合在一起,这里的Embedding特征包括了离散特征的Embedding结果以及原始的连续特征:
x0=[xembed,1T,⋯,xembed,kT,xdenseT]
得到Embedding层的结果后,便进入到DCN网络的核心的两个网络,分别是Cross network和Deep network。
2.2.2. Cross network
Cross network部分是Deep&Cross网络的核心部分,其作用是利用深度神经网络充分挖掘特征中的交叉特征。具体过程的形式化表示如下图所示:
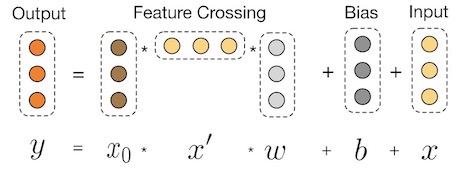
其具体的数学表述为:
xl+1=x0xlTwl+bl+xl=f(xl,wl,bl)+xl
其中,xl,xl+1∈Rd表示的是Cross network的第l层和第l+1层的输出向量,wl,bl∈Rd是Cross network的第l层的参数。上述公式的第二部分可以写成:
f(xl,wl,bl)=xl+1−xl
从上述公式可以看出是一个残差网络[3]的表达形式,函数f:Rd↦Rd需要拟合的是第l+1层和第l层的残差xl+1−xl。在ResNet中,残差网络的优点主要有:
- 通过残差网络可以构建深层网络。在传统的MLP,当网络加深之后,往往存在过拟合现象。而通过残差网络构建深层网络,可以减少过拟合现象的发生。
- 残差网络使用了ReLU激活函数取代Sigmoid激活函数可以有效防止梯度弥散,使得网络更容易收敛。
总的来说,可以通过残差网络构建更深层的模型,便于学习到特征之间的交叉属性。
2.2.3. Deep network
Deep network部分与Wide&Deep模型中一致,是一个典型的全连接前馈神经网络,其可以由下属公式表示:
hl+1=f(Wlhl+bl)
其中,hl∈Rnl,hl+1∈Rnl+1分别为第l层和第l+1层的隐含层输出,Wl∈Rnl+1×nl,bl∈Rnl+1为Deep network第l层到第l+1层的参数;f(⋅)是一个激活函数,如ReLU。
2.2.4. Combination
Combination层的作用是将上述两个network的结果组合在一起,以便送入到输出层,通常选择concat的方法将两者组合在一起,如[xL1T,hL2T],最终送入到输出层,输出层的结果为:
p=σ([xL1T,xL2T]wlogits)
其中,xL1T∈Rd,xL2T∈Rm分别为Cross network和Deep network的输出,wlogits为Combination层到输出层的权重,σ为激活函数σ=1+exp(−x)1。
2.3. Cross network中的特征交叉
Cross network中的特征交叉才是Cross network的核心,为了方便描述,在此对Cross network做一些限定:假设网络的深度L=2,输入x0∈Rd,为描述简单,假设d=2,此时x0T=[x0,0,x0,1],则L=1层的输出为:
x1=x0x0Tw0+b0+x0
其中,x0x0T为:
x0x0T=(x0,0x0,0x0,1x0,0x0,0x0,1x0,1x0,1)
由于x0∈Rd,w0∈Rd,则x0x0Tw0∈Rd,最终x1∈Rd。L=2层的输出为:
x2=x0x1Tw1+b1+x1=x0[x0x0Tw0+b0+x0]Tw1+b1+x0x0Tw0+b0+x0
从上述公式可以看到x1包含了原始特征x0从一阶(即:x0,0,x0,1)到二阶(即:x0,0x0,0,x0,0x0,1,x0,1x0,0和x0,1x0,1)的所有可能叉乘组合,而x2包含了其从一阶到三阶的所有可能叉乘组合。由此可知随着Cross network的网络深度的增加,交叉的阶数也在增加,通过这种方式实现特征之间的充分交叉,同时通过不同层的权重wi选择不同阶数的交叉特征,以此达到特征选择的效果。
注:在Cross network中,网络中每一层的维数都是相等的。
3. 总结
Deep&Cross Network通过对Cross network的设计,可以显示、自动地构造有限高阶的特征叉乘,并完成不同阶特征的选择,从而在一定程度上摆脱了人工的特征工程,同时保留深度网络起到一定的泛化作用。
参考文献
[1] Wang R, Fu B, Fu G, et al. Deep & cross network for ad click predictions[M]//Proceedings of the ADKDD’17. 2017: 1-7.
[2] Cheng H T, Koc L, Harmsen J, et al. Wide & Deep Learning for Recommender Systems[J]. 2016:7-10.
[3] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.

