1. 概述 特征交叉对于CTR问题的求解有着重要作用,纵观CTR模型的发展可以看出,每一次效果的提升,都伴随着对特征的挖掘,尤其是交叉特征。FM[1]算法在线性模型LR的基础上增加了二阶特征的交叉,对LR效果有着显著的提升;随着深度学习的发展,深度模型天然的特征交叉能力,Google的Wide & Deep[2]通过结合Wide模型的记忆能力和Deep模型的泛化能力,充分利用Deep侧的特征交叉能力,然而由于Wide侧使用的依然是线性模型,依赖于人工特征工程的参与。DeepFM[3]是华为在2017年提出的用于求解CTR问题的深度模型,DeepFM是在Google的Wide & Deep模型的基础上,将FM算法引入到Wide侧,替换掉原始的Wide & Deep模型中的LR模型,可以实现端到端的学习特征的交叉,无需人工特征工程的参与。DeepFM模型一经推出,就受到业界很多公司的关注,并在众多互联网公司的多个场景中落地。
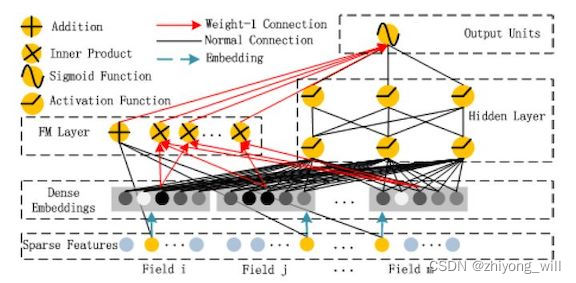
2. 算法原理 2.1. DeepFM的网络结构 DeepFM的网络结构如下图所示:
在DeepFM的网络结构中,主要包括四个部分:第一,Embedding层,用于将稀疏的离散特征转换成稠密的特征向量;第二,FM层,用于计算交叉特征,如上图中的左侧部分;第三,DNN部分,与Wide & Deep模型中的Deep侧一致;最后,输出层,融合左侧FM层和右侧DNN部分的输出得到最终的模型输出。
2.2. DeepFM的计算过程 2.2.1. Embedding层 Embedding层的作用是将输入样本中的稀疏特征转化成稠密的特征。假设训练集( χ , y ) \left ( \chi ,y \right ) ( χ , y ) n n n χ \chi χ m m m y ∈ { 0 , 1 } y\in \left \{ 0,1 \right \} y ∈ { 0 , 1 }
通过one-hot编码后,每一个样本( x , y ) \left ( x,y \right ) ( x , y ) x x x d d d x = [ x f i e l d 1 , x f i e l d 2 , ⋯ , x f i e l d j , ⋯ , x f i e l d m ] x=\left [ x_{field_1},x_{field_2},\cdots ,x_{field_j},\cdots ,x_{field_m} \right ] x = [ x f i e l d 1 , x f i e l d 2 , ⋯ , x f i e l d j , ⋯ , x f i e l d m ] x f i e l d j x_{field_j} x f i e l d j χ \chi χ j j j
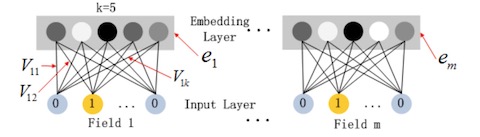
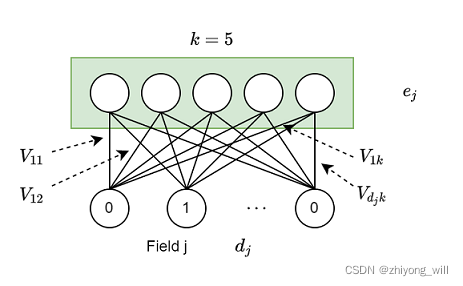
由上图可知,Embedding的过程是针对每个域单独进行的。为描述简单,假设对于第j j j x f i e l d j x_{field_j} x f i e l d j j j j d j d_j d j e j e_j e j k k k k = 5 k=5 k = 5
上述的映射可以由下述的公式表示:
e j = W j ⋅ x f i e l d j e_j=W_j\cdot x_{field_j} e j = W j ⋅ x f i e l d j
其中W j W_j W j k × d j k\times d_j k × d j
W j = ( V 11 V 21 ⋯ V d j 1 V 12 V 22 ⋯ V d j 2 ⋮ ⋮ ⋱ ⋮ V 1 k V 2 k ⋯ V d j k ) W_j=\begin{pmatrix}
V_{11} & V_{21} & \cdots & V_{d_j1}\\
V_{12} & V_{22} & \cdots & V_{d_j2}\\
\vdots & \vdots & \ddots & \vdots \\
V_{1k} & V_{2k} & \cdots & V_{d_jk}
\end{pmatrix} W j = V 11 V 12 ⋮ V 1 k V 21 V 22 ⋮ V 2 k ⋯ ⋯ ⋱ ⋯ V d j 1 V d j 2 ⋮ V d j k
其中,可以看到:
e j , 1 = V 11 ⋅ x f i e l d j , 1 + V 21 ⋅ x f i e l d j , 2 + ⋯ + V d j , 1 ⋅ x f i e l d j , d j e_{j,1}=V_{11}\cdot x_{field_j,1}+V_{21}\cdot x_{field_j,2}+\cdots +V_{d_j,1}\cdot x_{field_j,d_j} e j , 1 = V 11 ⋅ x f i e l d j , 1 + V 21 ⋅ x f i e l d j , 2 + ⋯ + V d j , 1 ⋅ x f i e l d j , d j
此处的V 11 V_{11} V 11 V d j k V_{d_jk} V d j k
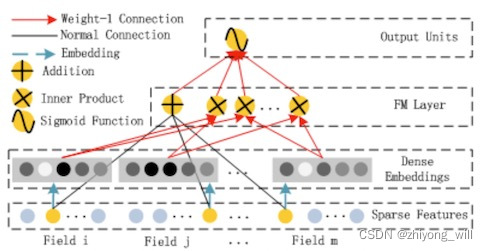
2.2.2. FM部分 FM算法是在2010年提出的具有二阶特征交叉的模型,FM算法模型结构如下图所示:
FM模型的表达式为:
y ^ = w 0 + ∑ i = 1 n w i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n ⟨ v i , v j ⟩ x i x j \hat{y}=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}\left \langle v_i,v_j \right \rangle x_ix_j y ^ = w 0 + i = 1 ∑ n w i x i + i = 1 ∑ n − 1 j = i + 1 ∑ n ⟨ v i , v j ⟩ x i x j
其中,⟨ v i , v j ⟩ = ∑ f = 1 k v i , f ⋅ v j , f \left \langle v_i,v_j \right \rangle=\sum_{f=1}^{k}v_{i,f}\cdot v_{j,f} ⟨ v i , v j ⟩ = ∑ f = 1 k v i , f ⋅ v j , f x x x i i i
y F M = ⟨ w , x ⟩ + ∑ j 1 = 1 d − 1 ∑ j 2 = j 1 + 1 d ⟨ V i , V j ⟩ x j 1 ⋅ x j 2 y_{FM}=\left \langle w,x \right \rangle+\sum_{j_1=1}^{d-1}\sum_{j_2=j_1+1}^{d}\left \langle V_i,V_j \right \rangle x_{j_1}\cdot x_{j_2} y FM = ⟨ w , x ⟩ + j 1 = 1 ∑ d − 1 j 2 = j 1 + 1 ∑ d ⟨ V i , V j ⟩ x j 1 ⋅ x j 2
其中,w ∈ R d w\in \mathbb{R}^d w ∈ R d V i ∈ R k V_i\in \mathbb{R}^k V i ∈ R k
对于上图中有几点说明:
⟨ w , x ⟩ \left \langle w,x \right \rangle ⟨ w , x ⟩
针对交叉特征,假设域i i i j j j i i i x f i e l d i = ( x f i e l d i , 1 , x f i e l d i , 2 , ⋯ , x f i e l d i , d i ) x_{field_i}=\left ( x_{field_i,1},x_{field_i,2},\cdots ,x_{field_i,d_i} \right ) x f i e l d i = ( x f i e l d i , 1 , x f i e l d i , 2 , ⋯ , x f i e l d i , d i ) j j j x f i e l d j = ( x f i e l d j , 1 , x f i e l d j , 2 , ⋯ , x f i e l d j , d j ) x_{field_j}=\left ( x_{field_j,1},x_{field_j,2},\cdots ,x_{field_j,d_j} \right ) x f i e l d j = ( x f i e l d j , 1 , x f i e l d j , 2 , ⋯ , x f i e l d j , d j ) x f i e l d i , i ≠ 0 x_{field_i,i}\neq 0 x f i e l d i , i = 0 x f i e l d j , j ≠ 0 x_{field_j,j}\neq 0 x f i e l d j , j = 0 i i i j j j x f i e l d i , i x_{field_i,i} x f i e l d i , i x f i e l d j , j x_{field_j,j} x f i e l d j , j
⟨ V i , V j ⟩ x j 1 ⋅ x j 2 = ( V i , 1 f i l e d i ⋅ V j , 1 f i l e d j + ⋯ + V i , k f i l e d i ⋅ V j , k f i l e d j ) ⋅ x f i e l d i , i ⋅ x f i e l d j , j \left \langle V_i,V_j \right \rangle x_{j_1}\cdot x_{j_2}=\left ( V_{i,1}^{filed_i}\cdot V_{j,1}^{filed_j}+\cdots +V_{i,k}^{filed_i}\cdot V_{j,k}^{filed_j} \right )\cdot x_{field_i,i}\cdot x_{field_j,j} ⟨ V i , V j ⟩ x j 1 ⋅ x j 2 = ( V i , 1 f i l e d i ⋅ V j , 1 f i l e d j + ⋯ + V i , k f i l e d i ⋅ V j , k f i l e d j ) ⋅ x f i e l d i , i ⋅ x f i e l d j , j
即为:
V i , 1 f i l e d i ⋅ x f i e l d i , i ⋅ V j , 1 f i l e d j ⋅ x f i e l d j , j + ⋯ + V i , k f i l e d i ⋅ x f i e l d i , i ⋅ V j , k f i l e d j ⋅ x f i e l d j , j V_{i,1}^{filed_i}\cdot x_{field_i,i}\cdot V_{j,1}^{filed_j}\cdot x_{field_j,j}+\cdots +V_{i,k}^{filed_i}\cdot x_{field_i,i}\cdot V_{j,k}^{filed_j}\cdot x_{field_j,j} V i , 1 f i l e d i ⋅ x f i e l d i , i ⋅ V j , 1 f i l e d j ⋅ x f i e l d j , j + ⋯ + V i , k f i l e d i ⋅ x f i e l d i , i ⋅ V j , k f i l e d j ⋅ x f i e l d j , j
此时,域i i i j j j
e i , m = V i , m f i e l d i ⋅ x f i e l d i , i e_{i,m}=V_{i,m}^{field_i}\cdot x_{field_i,i} e i , m = V i , m f i e l d i ⋅ x f i e l d i , i
e j , m = V j , m f i e l d j ⋅ x f i e l d j , j e_{j,m}=V_{j,m}^{field_j}\cdot x_{field_j,j} e j , m = V j , m f i e l d j ⋅ x f i e l d j , j
其中m = 1 ∼ k m=1\sim k m = 1 ∼ k
e i , 1 ⋅ e j , 1 + ⋯ + e i , k ⋅ e j , k e_{i,1}\cdot e_{j,1}+\cdots +e_{i,k}\cdot e_{j,k} e i , 1 ⋅ e j , 1 + ⋯ + e i , k ⋅ e j , k
这也就验证了上图中Weight-1 Connection。
2.2.3. Deep部分 与Wide & Deep模型一致,Deep部分是一个传统的DNN模型,其基本的结构如下图所示:
输入的稀疏特征经过Embedding层后得到稠密的特征表示,该稠密特征可以作为DNN模型的输入:
a ( 0 ) = [ e 1 , e 2 , ⋯ , e m ] a^{\left ( 0 \right )}=\left [ e_1,e_2,\cdots ,e_m \right ] a ( 0 ) = [ e 1 , e 2 , ⋯ , e m ]
其中,e i e_i e i i i i a ( 0 ) a^{\left ( 0 \right )} a ( 0 ) l + 1 l+1 l + 1
a ( l + 1 ) = σ ( W ( l ) a ( l ) + b ( l ) ) a^{\left ( l+1 \right )}=\sigma \left ( W^{\left (l \right )}a^{\left ( l \right )} +b^{\left ( l \right )}\right ) a ( l + 1 ) = σ ( W ( l ) a ( l ) + b ( l ) )
其中,l l l σ \sigma σ W ( l ) W^{\left (l \right )} W ( l ) b ( l ) b^{\left ( l \right )} b ( l )
y D N N = σ ( W ∣ H ∣ + 1 ⋅ a H + b ∣ H ∣ + 1 ) y_{DNN}=\sigma \left ( W^{\left | H \right |+1}\cdot a^H+b^{\left | H \right |+1} \right ) y D NN = σ ( W ∣ H ∣ + 1 ⋅ a H + b ∣ H ∣ + 1 )
其中,∣ H ∣ \left | H \right | ∣ H ∣
2.2.4. 网络输出 在DeepFM中,分别由左侧的FM模型得到了FM部分的输出y F M y_{FM} y FM y D N N y_{DNN} y D NN
y ^ = s i g m o i d ( y F M + y D N N ) \hat{y}=sigmoid\left ( y_{FM}+y_{DNN} \right ) y ^ = s i g m o i d ( y FM + y D NN )
3. 总结 在DeepFM网络中,通过将Wide & Deep模型中的Wide侧模型替换成FM模型,实现自动的交叉特征选择,从而实现无需人工参与就可以通过模型进行端到端的学习,自动学习到各种层级的交叉特征。
参考文献 [1] Rendle S . Factorization Machines[C]// ICDM 2010, The 10th IEEE International Conference on Data Mining, Sydney, Australia, 14-17 December 2010. IEEE, 2010.
[2] Cheng H T, Koc L, Harmsen J, et al. Wide & Deep Learning for Recommender Systems[J]. 2016:7-10.
[3] Guo H, Tang R, Ye Y, et al. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction[J]. 2017:1725-1731.
[4] CTR预估算法之FM, FFM, DeepFM及实践
[5] 推荐系统遇上深度学习(三)–DeepFM模型理论和实践
[6] tensorflow-DeepFM