1. 概述

Neural Factorization Machines（NFM）[1]是在2017年提出的用于求解CTR问题的算法模型，在Wide & Deep模型被提出后，相继出现了一些改进的算法模型，如DeepFM和DCN可以看成是对于Wide & Deep模型中Wide部分的改进，而此处的NFM模型则是可以看作是对Deep部分的改进。从模型的名字来看，NFM包含了两个部分，第一为Neural，这部分与神经网络相关，第二为Factorization Machines，这部分与FM相关。对于FM模型，文章中提到了可以从深度学习网络结构的角度来看待，此时FM就可以看作是由单层LR和二阶特征交叉组成的Wide & Deep模型，与Google提出的Wide & Deep模型的不同之处就是Deep部分是二阶隐向量相乘。从这个角度上来看，NFM是在FM的基础上利用NN模型代替FM中的Deep部分，而这个NN与Wide & Deep中的Deep的不同是NFM中的Deep中包含了Bi-Interaction的层，用于对特征做二阶交叉运算。综上，NFM的优化点主要为：

1. 在深度网络中引入Bi-Interaction做进一步的特征交叉。
2. 对比FM，深度网络能够学习更高阶的非线形的特征交叉。

2. 算法原理

2.1. NFM模型的网络结构

完整的NFM的网络结构如下图所示：

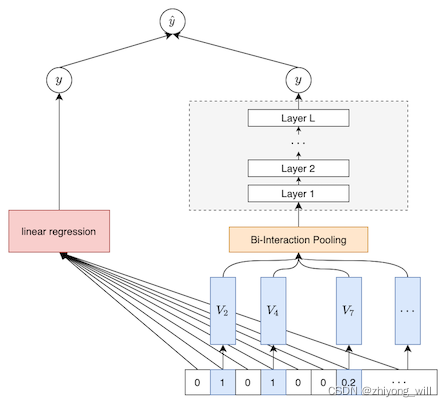
对于NFM模型，假设输入的稀疏经one-hot编码后的向量为$\mathbf{x}\in \mathbb{R}^n$，NFM模型的输出为：

$$\hat{y}_{NFM}\left ( \mathbf{x} \right )=w_0+\sum_{i=1}^{n}w_ix_i+f\left ( \mathbf{x} \right )$$

其中，$w_0+\sum_{i=1}^{n}w_ix_i$如上图中的linear regression，$f\left ( \mathbf{x} \right )$为上图中的右半部分。对于FM算法，其表达式为：

$$\hat{y}_{FM}\left ( \mathbf{x} \right )=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}\left \langle v_i,v_j \right \rangle x_ix_j$$

从两者的数学表达式可以看出，FM模型是NFM的特殊形式，即满足：$f\left ( \mathbf{x} \right )=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}\left \langle v_i,v_j \right \rangle x_ix_j$。我们发现如何构造$f\left ( \mathbf{x} \right )$式NFM模型中的关键部分。

2.2. NFM模型中的特征交叉

NFM模型中的特征交叉$f\left ( \mathbf{x} \right )$的结构如下图所示：

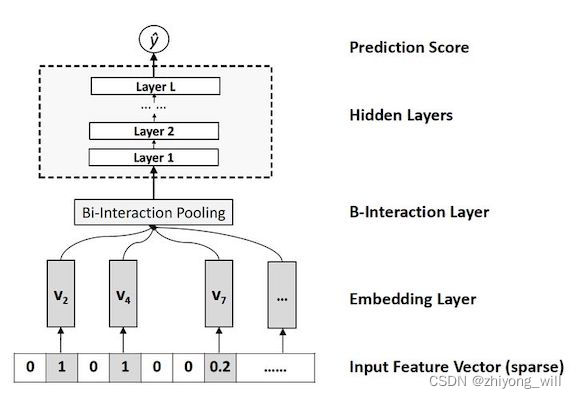
如上图，NFM中特征交叉部分$f\left ( \mathbf{x} \right )$是一个深度神经网络模型，在特征交叉部分$f\left ( \mathbf{x} \right )$的网络中，主要包括Embedding层，Bi-Interaction层，隐含层以及预测层。

2.2.1. Embedding层

Embedding层的作用是将稀疏的one-hot特征转换成稠密的向量表示，这个操作是深度神经网络的必备操作方法。假设转换后的embeding向量为：

$$\mathbf{V}_x=\left\{x_1\mathbf{v}_1,\cdots ,x_n\mathbf{v}_n \right\}$$

2.2.2. Bi-Interaction层

对稀疏特征处理后就可以进入到深度学习模型的计算中，在NFM中，首先进入到Bi-Interaction层中，Bi-Interaction Pooling的主要作用是对Embedding后的特征学习特征交叉，其具体格式为：

$$f_{BI}\left ( \mathbf{V}_x \right )=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}x_i\mathbf{v}_i\odot x_j\mathbf{v}_j$$

其中，$\odot$表示的是两个向量的元素乘积，即$\left ( \mathbf{v}_i\odot \mathbf{v}_j \right )_k=v_{ik}v_{jk}$。可以看到Bi-Interaction的输出为两个向量的交叉。

2.2.3. Hidden层

在Bi-Interaction层之上是堆叠了一系列的隐含层，主要的目的是学习更高阶的特征交叉，用数学的表述为：

$$\begin{matrix} \mathbf{z}_1=\sigma _1\left ( \mathbf{W}_1f_{BI}\left ( \mathbf{V}_x \right )+\mathbf{b}_1 \right )\\ \mathbf{z}_2=\sigma _2\left ( \mathbf{W}_2\mathbf{z}_1+\mathbf{b}_2 \right )\\ \cdots \cdots \\ \mathbf{z}_L=\sigma _L\left ( \mathbf{W}_L\mathbf{z}_{L-1}+\mathbf{b}_L \right ) \end{matrix}$$

其中，$L$表示的是隐含层的层数，$\mathbf{W}_L$，$\mathbf{b}_L$和$\sigma _L$分别为第$L$的网络权重，偏置和激活函数。

2.2.4. Prediction层

经过多个隐含层后，得到隐含层的输出$\mathbf{z}_L$，最终将隐含层的输出送入到预测层中，得到Deep侧的输出结果，即为：

$$f\left ( \mathbf{x} \right )=\mathbf{h}^T\mathbf{z}_L$$

其中，$\mathbf{h}$为输出层的权重，最终NFM模型的输出结果为：

$$\hat{y}_{NFM}\left ( \mathbf{x} \right )=w_0+\sum_{i=1}^{n}w_ix_i+\mathbf{h}^T\sigma _L\left ( \mathbf{W}_L\left ( \cdots \sigma _1\left ( \mathbf{W}_1f_{BI}\left ( \mathbf{V}_x \right )+\mathbf{b}_1 \right )\cdots \right )+\mathbf{b}_L \right )$$

其中，$\Theta =\left \{ w_0,\left \{ w_i,\mathbf{v}_i \right \},\mathbf{h},\left \{ \mathbf{W}_l,\mathbf{b}_l \right \} \right \}$为模型的参数。

3. 总结

通过上述的拆分会发现NFM与FM以及Wide & Deep模型之间有着很大的相似性，不同在于NFM中不光包含了FM中的二阶特征，同时利用DNN的特性构造更高阶非线性的交叉，总体而言，主要还是集中在特征交叉的工作上。

参考文献

[1] He X , Chua T S . Neural Factorization Machines for Sparse Predictive Analytics[J]. ACM SIGIR FORUM, 2017, 51(cd):355-364.