生成对抗网络GAN

 CV   |  2022年05月06日   |  阅读：999次

1. 概述

生成对抗网络GAN（Generative adversarial nets）[1]是由Goodfellow等人于2014年提出的基于深度学习模型的生成框架，可用于多种生成任务。从名称也不难看出，在GAN中包括了两个部分，分别为”生成”和“对抗”，整两个部分也分别对应了两个网络，即生成网络（Generator）GG和判别网络（Discriminator）DD，为描述简单，以图像生成为例：

  • 生成网络（Generator）GG用于生成图片，其输入是一个随机的噪声z\boldsymbol{z}，通过这个噪声生成图片，记作G(z)G\left ( \boldsymbol{z} \right )
  • 判别网络（Discriminator）DD用于判别一张图片是否是真实的，对应的，其输入是一整图片x\boldsymbol{x}，输出D(x)D\left ( \boldsymbol{x} \right )表示的是图片x\boldsymbol{x}为真实图片的概率

在GAN框架的训练过程中，希望生成网络GG生成的图片尽量真实，能够欺骗过判别网络DD；而希望判别网络DD能够把GG生成的图片从真实图片中区分开。这样的一个过程就构成了一个动态的“博弈”。最终，GAN希望能够使得训练好的生成网络GG生成的图片能够以假乱真，即对于判别网络DD来说，无法判断GG生成的网络是不是真实的。

综上，训练好的生成网络GG便可以用于生成“以假乱真”的图片。

2. 算法原理

2.1. GAN的框架结构

GAN的框架是由生成网络GG和判别网络DD这两种网络结构组成，通过两种网络的“对抗”过程完成两个网络的训练，GAN框架由下图所示：

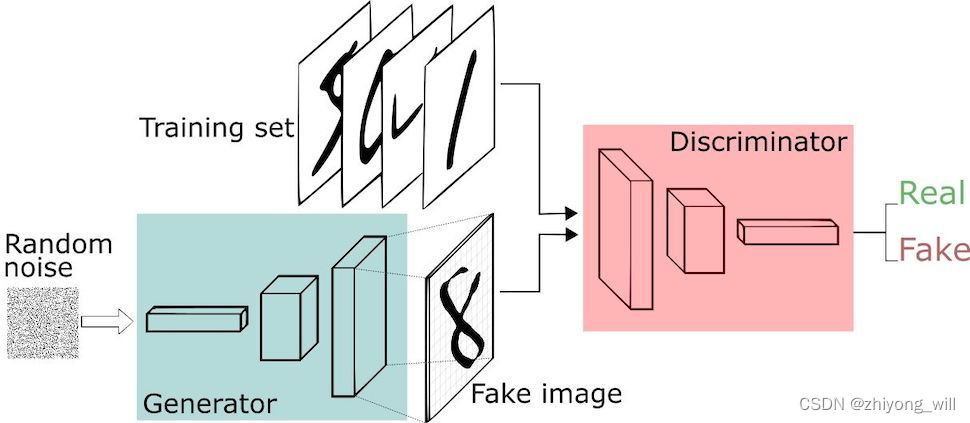
在这里插入图片描述

由生成网络GG生成一张“Fake image”，判别网络DD判断这张图片是否来自真实图片。

2.2. GAN框架的训练过程

在GAN的训练过程中，其最终的目标是使得训练出来的生成模型GG生成的图片与真实图片具有相同的分布，其过程可通过下图描述[2]：

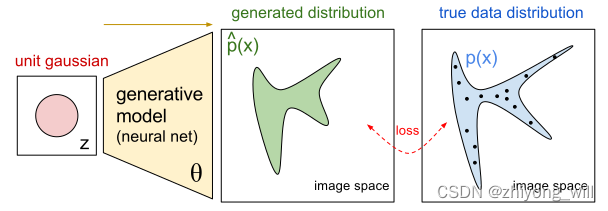
在这里插入图片描述

假设有一个先验分布pz(z)p_{\boldsymbol{z}}\left ( \boldsymbol{z} \right )，如上图中的unit gaussian，通过采样得到其中的一个样本点z\boldsymbol{z}。对于真实的图片，事先对于其分布是未知的，即上图中的p(x)p\left ( \boldsymbol{x} \right )未知。为了使得能与真实图片具有相同的分布，通过一个生成模型将先验分布映射到另一个分布，生成模型记为G(z;θg)G\left ( \boldsymbol{z};\theta _g \right )，其中θg\theta _g为生成模型的参数，这里的生成模型可以是一个前馈神经网络MLP，θg\theta _g便为该神经网络的参数。通过多次的采样，便可以刻画出生成的分布p^(x)\hat{p}\left ( \boldsymbol{x} \right )，此时需要计算其与真实的分布p(x)p\left ( \boldsymbol{x} \right )之间的相关性，即需要一个判别模型来定量表示两个分布之间的相关性，这里可以通过另一个前馈神经网络MLP，判别模型记为D(x;θd)D\left ( \boldsymbol{x};\theta _d \right )，其中D(x;θd)D\left ( \boldsymbol{x};\theta _d \right )的输出是一个标量，表示的是x\boldsymbol{x}来自真实的分布，而不是来自于生成模型构造出的分布的概率。

对于这样的一个过程中，有两个模型，分别为生成模型G(z;θg)G\left ( \boldsymbol{z};\theta _g \right )和判别模型D(x;θd)D\left ( \boldsymbol{x};\theta _d \right )，在GAN中，生成模型和判断模型分别对应了一个神经网络，以下都称为生成网络和判别模型。GAN希望的是对于判别网络，其能够正确判定数据是否来自真实的分布，对于生成网络，其能够尽可能使得生成的数据能够“以假乱真”，使得判别网络分辨不了。这样的训练过程是一个动态的“博弈”过程，通过交替训练，最终使得生成网络GG生成的图片能够“以假乱真”，其具体过程如下图所示：

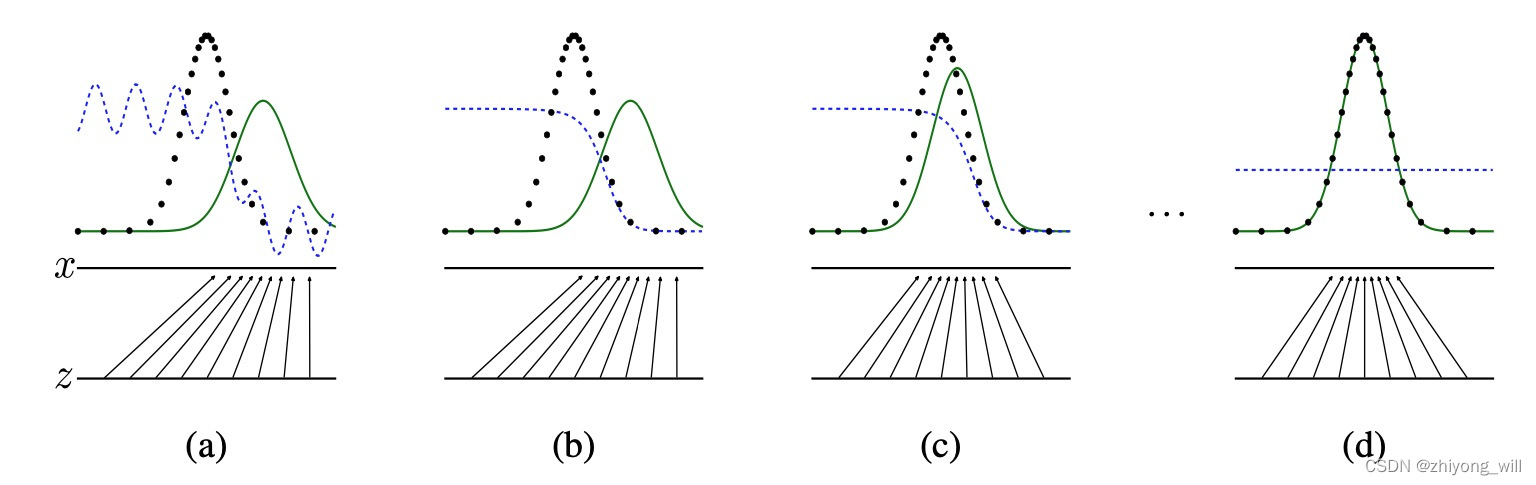
在这里插入图片描述

如上图(a)中，黑色的虚线表示的是从真实的分布pxp_{\boldsymbol{x}}，绿色的实线表示的是需要训练的生成网络的生成的分布pg(G)p_g\left ( G \right )，蓝色的虚线表示的是判别网络，最下面的横线z\boldsymbol{z}表示的是从一个先验分布（如图中是一个均匀分布）采样得到的数据点，中间的横线x\boldsymbol{x}表示的真实分布，两条横线之间的对应关系表示的是生成网络将先验分布映射成一个生成分布pg(G)p_g\left ( G \right )。从图(a)到图(d)表示了一个完整的交替训练过程，首先，如图(a)所示，当通过先验分布采样后的数据经过生成网络GG映射后得到了图上绿色的实线代表的分布，此时判别网络DD并不能区分数据是否来自真实数据，通过对判别网络的训练，其能够正确地判断生成的数据是否来自真实数据，如图(b)所示；此时更新生成网络GG，通过对先验分布重新映射到新的生成分布上，如图(c)中的绿色实线所示。依次交替完成上述步骤，当达到一定迭代的代数后，达到一个平衡状态，此时pg=pdatap_g=p_{data}，判别网络DD将不能区分图片是否来自真实分布，且D(x)=12D\left ( \boldsymbol{x} \right )=\frac{1}{2}。

2.3. 价值函数

对于GAN框架，其价值函数V(G,D)V\left ( G,D \right )为：

minG  maxD  V(D,G)=Ex∼pdata(x)[log  D(x)]+Ez∼pz(z)[log  (1−D(G(z)))]\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )=\mathbb{E}_{\boldsymbol{x}\sim p_{data}\left ( \boldsymbol{x} \right )}\left [ log\; D\left ( \boldsymbol{x} \right ) \right ]+\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}\left ( \boldsymbol{z} \right )}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z} \right ) \right ) \right ) \right ]

其中，Ex∼pdata(x)[log  D(x)]\mathbb{E}_{\boldsymbol{x}\sim p_{data}\left ( \boldsymbol{x} \right )}\left [ log\; D\left ( \boldsymbol{x} \right ) \right ]表示的是log  D(x)log\; D\left ( \boldsymbol{x} \right )的期望，同理，Ez∼pz(z)[log  (1−D(G(z)))]\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}\left ( \boldsymbol{z} \right )}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z} \right ) \right ) \right ) \right ]表示的是log  (1−D(G(z)))log\; \left ( 1-D\left ( G\left ( \boldsymbol{z} \right ) \right ) \right )的期望。

假设从真实数据中采样mm个样本{x(1),x(2),⋯ ,x(m)}\left \{ \boldsymbol{x}^{\left ( 1 \right )},\boldsymbol{x}^{\left ( 2 \right )},\cdots ,\boldsymbol{x}^{\left ( m \right )} \right \}，从噪音分布pg(z)p_g\left ( \boldsymbol{z} \right )中同样采样mm个样本，记为{z(1),z(2),⋯ ,z(m)}\left \{ \boldsymbol{z}^{\left ( 1 \right )},\boldsymbol{z}^{\left ( 2 \right )},\cdots ,\boldsymbol{z}^{\left ( m \right )} \right \}，此时，上述价值函数可以近似表示为：

minG  maxD  V(D,G)≈∑i=1m[log  D(x(i))]+∑i=1m[log  (1−D(G(z(i))))]\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )\approx \sum_{i=1}^{m}\left [ log\; D\left ( \boldsymbol{x}^{\left ( i \right )} \right ) \right ]+\sum_{i=1}^{m}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )} \right ) \right ) \right ) \right ]

简化后为：

minG  maxD  V(D,G)≈∑i=1m[log  D(x(i))+log  (1−D(G(z(i))))]\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )\approx \sum_{i=1}^{m}\left [ log\; D\left ( \boldsymbol{x}^{\left ( i \right )} \right ) + log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )} \right ) \right ) \right ) \right ]

上述的交替训练过程如下流程所示：

在这里插入图片描述

3. GAN背后的数学原理

为了能够从数学的角度对上述过程做分析，首先对问题进行数学的描述：假设真实的数据分布为pdata(x)p_{data}\left ( \boldsymbol{x} \right )，生成网络得到的分布为pg(x;θ)p_g\left ( \boldsymbol{x};\theta \right )，其中θ\theta为生成网络的参数，现在需要找到一个θ∗\theta ^{\ast }使得pg(x;θ)≈pdata(x)p_g\left ( \boldsymbol{x};\theta \right )\approx p_{data}\left ( \boldsymbol{x} \right )。

3.1. 为什么会有这样的价值函数

由上可知，当生成网络GG确定后，GAN的价值函数可以近似为：

maxD  V(D)≈∑i=1m[log  D(x(i))]+∑i=1m[log  (1−D(G(z(i))))]\underset{D}{max}\; V\left ( D \right )\approx \sum_{i=1}^{m}\left [ log\; D\left ( \boldsymbol{x}^{\left ( i \right )} \right ) \right ]+\sum_{i=1}^{m}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )} \right ) \right ) \right ) \right ]

其来源可以追溯到二分类的损失函数，对于一个二分类来说，通常选择交叉墒作为其损失函数，交叉墒的一般形式为：

J(θ)=−1m∑i=1m[y(i)log  y^(i)+(1−y(i))log  (1−y^(i))]J\left ( \theta \right )=-\frac{1}{m}\sum_{i=1}^{m}\left [ y^{\left ( i \right )}log\; \hat{y}^{\left ( i \right )}+\left ( 1-y^{\left ( i \right )} \right )log\; \left ( 1-\hat{y}^{\left ( i \right )} \right ) \right ]

其中，y(i)y^{\left ( i \right )}表示的是真实的样本标签，y^(i)\hat{y}^{\left ( i \right )}表示的是模型的预测值。对于GAN来说，样本分为两个部分，一个是来自真实的样本{(x(1),1),(x(2),1),⋯ ,(x(m),1)}\left \{ \left ( \boldsymbol{x}^{\left ( 1 \right )},1 \right ),\left ( \boldsymbol{x}^{\left ( 2 \right )},1 \right ),\cdots ,\left ( \boldsymbol{x}^{\left ( m \right )},1 \right ) \right \}，将其带入到交叉墒的公式中（去除交叉墒的负号）为：

=1m∑i=1m[1⋅log  D(x(i))+(1−1)log  (1−D(x(i)))]=1m∑i=1m[log  D(x(i))]\begin{aligned} &= \frac{1}{m}\sum_{i=1}^{m}\left [ 1\cdot log\; D\left ( \boldsymbol{x}^{\left ( i \right )} \right )+\left ( 1-1 \right )log\; \left ( 1-D\left ( \boldsymbol{x}^{\left ( i \right )} \right ) \right ) \right ]\\ &= \frac{1}{m}\sum_{i=1}^{m}\left [ log\; D\left ( \boldsymbol{x}^{\left ( i \right )} \right )\right ] \end{aligned}

另一个则是来时生成模型{(G(z(1)),0),(G(z(2)),0),⋯ ,(G(z(m)),0)}\left \{ \left ( G\left ( \boldsymbol{z}^{\left ( 1 \right )} \right ),0 \right ),\left ( G\left ( \boldsymbol{z}^{\left ( 2 \right )} \right ),0 \right ),\cdots ,\left ( G\left ( \boldsymbol{z}^{\left ( m \right )} \right ),0 \right ) \right \}，将其带入到交叉墒的公式中（去除交叉墒的负号）为:

=1m∑i=1m[0⋅log  D(G(z(i)))+(1−0)⋅log  (1−D(G(z(i))))]=1m∑i=1m[log  (1−D(G(z(i))))]\begin{aligned} &= \frac{1}{m}\sum_{i=1}^{m}\left [ 0\cdot log\; D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )} \right ) \right ) + \left ( 1-0 \right )\cdot log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )} \right ) \right ) \right ) \right ]\\ &= \frac{1}{m}\sum_{i=1}^{m}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )} \right ) \right ) \right ) \right ] \end{aligned}

将两部分合并在一起，便是上述的价值函数。

3.2. KL散度

需要刻画两个分布是否相似，需要用到KL散度（KL divergence）。KL散度是统计学中的一个基本概念，用于衡量两个分布的相似程度，数值越小，表示两种概率分布越接近。对于离散的概率分布，定义如下：

DKL(P∥Q)=∑iP(i)logP(i)Q(i)D_{KL}\left ( P\parallel Q \right )=\sum_{i}P\left ( i \right )log\frac{P\left ( i \right )}{Q\left ( i \right )}

对于连续的概率分布，定义如下：

DKL(P∥Q)=∫−∞+∞p(x)logp(x)q(x)dxD_{KL}\left ( P\parallel Q \right )=\int_{-\infty }^{+\infty }p\left ( x \right )log\frac{p\left ( x \right )}{q\left ( x \right )}dx

3.3. 极大似然估计

极大似然估计（Maximum Likelihood Estimation），是一种概率论在统计学的应用，它是参数估计的方法之一。上述需要求解生成分布pg(x;θ)p_g\left ( \boldsymbol{x};\theta \right )中的参数θ\theta，需要用到极大似然估计。根据极大似然估计的方式，由于最终是希望生成的分布pg(x;θ)p_g\left ( \boldsymbol{x};\theta \right )与原始的真实分布pdata(x)p_{data}\left ( \boldsymbol{x} \right )，首先从真实分布pdata(x)p_{data}\left ( \boldsymbol{x} \right )采样mm个数据点，记为{x(1),x(2),⋯ ,x(m)}\left \{ \boldsymbol{x}^{\left ( 1 \right )},\boldsymbol{x}^{\left ( 2 \right )},\cdots ,\boldsymbol{x}^{\left ( m \right )} \right \}，根据生成的分布，得到似然函数为：

L=∏i=1mpg(x(i);θ)L=\prod_{i=1}^{m}p_g\left ( \boldsymbol{x}^{\left ( i \right )};\theta \right )

取log后，得到等价的log似然：

L=∑i=1mlog  pg(x(i);θ)L=\sum_{i=1}^{m}log\; p_g\left ( \boldsymbol{x}^{\left ( i \right )};\theta \right )

此时，θ∗\theta ^{\ast }为：

θ∗=argmaxθ∑i=1mlog  pg(x(i);θ)≈argmaxθ  Ex∼pdata[log  pg(x;θ)]=argmaxθ∫xpdata(x)log  pg(x;θ)dx\begin{aligned} \theta ^{\ast }&=\underset{\theta }{argmax}\sum_{i=1}^{m}log\; p_g\left ( \boldsymbol{x}^{\left ( i \right )};\theta \right ) \\ &\approx \underset{\theta }{argmax}\; \mathbb{E}_{\boldsymbol{x}\sim p_{data}}\left [ log\; p_g\left ( \boldsymbol{x};\theta \right ) \right ] \\ &= \underset{\theta }{argmax}\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; p_g\left ( \boldsymbol{x};\theta \right )d\boldsymbol{x} \end{aligned}

对上述的公式做一些修改，增加一个与θ\theta无关的项∫xpdata(x)log  pdata(x)dx\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; p_{data}\left ( \boldsymbol{x} \right )d\boldsymbol{x}，这样并不改变对θ∗\theta ^{\ast }的求解，此时，公式变为：

argmaxθ∫xpdata(x)log  pg(x;θ)dx−∫xpdata(x)log  pdata(x)dx\underset{\theta }{argmax}\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; p_g\left ( \boldsymbol{x};\theta \right )d\boldsymbol{x}-\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; p_{data}\left ( \boldsymbol{x} \right )d\boldsymbol{x}

将最大值求解变成最小值为：

argminθ∫xpdata(x)log  pdata(x)dx−∫xpdata(x)log  pg(x;θ)dx\underset{\theta }{argmin}\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; p_{data}\left ( \boldsymbol{x} \right )d\boldsymbol{x}-\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; p_g\left ( \boldsymbol{x};\theta \right )d\boldsymbol{x}

通过积分公式的合并，得到：

argminθ∫xpdata(x)log  pdata(x)log  pg(x;θ)dx\underset{\theta }{argmin}\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\;\frac{p_{data}\left ( \boldsymbol{x} \right )}{log\; p_g\left ( \boldsymbol{x};\theta \right )} d\boldsymbol{x}

由KL散度可知，上述可以表示为：

argminθ  KL(pdata(x)∥pg(x;θ))\underset{\theta }{argmin}\; KL\left ( p_{data}\left ( \boldsymbol{x} \right )\parallel p_g\left ( \boldsymbol{x};\theta \right ) \right )

由此可以看出最小化KL散度等价于最大化似然函数。

3.4. 收敛性分析

当生成网络GG确定后，价值函数可以表示为：

maxD  V(D)=∫xpdata(x)log  (D(x))dx+∫zpz(z)log  (1−D(G(z)))dz=∫xpdata(x)log  (D(x))+pg(x)log  (1−D(x))dx\begin{aligned} \underset{D}{max}\; V\left ( D \right )&=\int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; \left ( D\left ( \boldsymbol{x} \right ) \right ) d\boldsymbol{x}+\int _{\boldsymbol{z}} p_{\boldsymbol{z}}\left ( \boldsymbol{z} \right )log\; \left ( 1-D\left ( G\left ( \boldsymbol{z} \right ) \right ) \right )d\boldsymbol{z} \\ &= \int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; \left ( D\left ( \boldsymbol{x} \right ) \right )+p_{g}\left ( \boldsymbol{x} \right )log\; \left ( 1-D\left ( \boldsymbol{x} \right ) \right ) d\boldsymbol{x} \end{aligned}

由于上述的积分与DD无关，上述可以简化成求解：

maxD[pdata(x)log  (D(x))+pg(x)log  (1−D(x))] \underset{D}{max}\left [ p_{data}\left ( \boldsymbol{x} \right )log\; \left ( D\left ( \boldsymbol{x} \right ) \right )+p_{g}\left ( \boldsymbol{x} \right )log\; \left ( 1-D\left ( \boldsymbol{x} \right ) \right )\right ]

求导数并令其为00，便可以得到最大的DD:

D∗=pdata(x)pdata(x)+pg(x)D^{\ast }=\frac{p_{data}\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}

且D(x)∈[0,1]D\left ( \boldsymbol{x} \right )\in \left [ 0,1 \right ]，将其带入到价值函数中，可得

V(D∗,G)=Ex∼pdata(x)[log  pdata(x)pdata(x)+pg(x)]+Ex∼pg(x)[log  (1−pdata(x)pdata(x)+pg(x))]V\left ( D^{\ast },G \right )=\mathbb{E}_{\boldsymbol{x}\sim p_{data}\left ( \boldsymbol{x} \right )}\left [ log\; \frac{p_{data}\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )} \right ]+\mathbb{E}_{\boldsymbol{x}\sim p_g\left ( \boldsymbol{x} \right )}\left [ log\; \left ( 1-\frac{p_{data}\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )} \right ) \right ]

对上式简化，可得：

V(D∗,G)=Ex∼pdata(x)[log  pdata(x)pdata(x)+pg(x)]+Ex∼pg(x)[log  pg(x)pdata(x)+pg(x)]=∫xpdata(x)log  pdata(x)pdata(x)+pg(x)dx+∫xpg(x)log  pg(x)pdata(x)+pg(x)dx\begin{aligned} V\left ( D^{\ast },G \right ) &= \mathbb{E}_{\boldsymbol{x}\sim p_{data}\left ( \boldsymbol{x} \right )}\left [ log\; \frac{p_{data}\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )} \right ]+\mathbb{E}_{\boldsymbol{x}\sim p_g\left ( \boldsymbol{x} \right )}\left [ log\; \frac{p_g\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )} \right ]\\ &= \int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; \frac{p_{data}\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}d\boldsymbol{x}+\int _{\boldsymbol{x}}p_g\left ( \boldsymbol{x} \right )log\; \frac{p_g\left ( \boldsymbol{x} \right )}{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}d\boldsymbol{x} \end{aligned}

通过对分子和分母分别除22，可得：

V(D∗,G)=∫xpdata(x)log  12pdata(x)pdata(x)+pg(x)2dx+∫xpg(x)log  12pg(x)pdata(x)+pg(x)2dx=−2log  2+KL(pdata(x)∥pdata(x)+pg(x)2)+KL(pg(x)∥pdata(x)+pg(x)2)\begin{aligned} V\left ( D^{\ast },G \right ) &= \int _{\boldsymbol{x}}p_{data}\left ( \boldsymbol{x} \right )log\; \frac{\frac{1}{2}p_{data}\left ( \boldsymbol{x} \right )}{\frac{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}{2}}d\boldsymbol{x}+\int _{\boldsymbol{x}}p_g\left ( \boldsymbol{x} \right )log\; \frac{\frac{1}{2}p_g\left ( \boldsymbol{x} \right )}{\frac{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}{2}}d\boldsymbol{x}\\ &= -2log\; 2+KL\left ( p_{data}\left ( \boldsymbol{x} \right )\parallel \frac{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}{2} \right )+KL\left ( p_g\left ( \boldsymbol{x} \right )\parallel \frac{p_{data}\left ( \boldsymbol{x} \right )+p_{g}\left ( \boldsymbol{x} \right )}{2} \right ) \end{aligned}

这里引入另一个符号：JS散度（Jensen-Shannon Divergence）

JSD(P∥Q)=12[KL(P∥M)+KL(Q∥M)]JSD\left ( P\parallel Q \right )=\frac{1}{2}\left [ KL\left ( P\parallel M \right ) + KL\left ( Q\parallel M \right )\right ]

其中，M=P+Q2M=\frac{P+Q}{2}。因此V(D∗,G)V\left ( D^{\ast },G \right )可以表示为：

V(D∗,G)=−2log  2+2JSD(pdata(x)∥pg(x))V\left ( D^{\ast },G \right )=-2log\; 2+2JSD\left ( p_{data}\left ( \boldsymbol{x} \right )\parallel p_g\left ( \boldsymbol{x} \right ) \right )

已知JS散度是一个非负值，且值域为[0,1]\left [ 0,1 \right ]，当两个分布相同时取00，不同时取11。对于V(D∗,G)V\left ( D^{\ast },G \right )的最小值为当JS=0JS=0时，即最小值是−2log  2-2log\; 2。此时pdata(x)=pg(x)p_{data}\left ( \boldsymbol{x} \right )=p_g\left ( \boldsymbol{x} \right )，此时求得的生成网络GG生成的数据分布与真实的数据分布差异性最小，即GAN所要求的目标：pg=pdatap_g=p_{data}。

3. 总结

生成对抗网络GAN中通过生成网络GG和判别网络DD之间的“生成”和“对抗”过程，通过多次的迭代，最终达到平衡，使得训练出来的生成网络GG能够生成“以假乱真”的数据，判别网络DD不能将其从真实数据中区分开。

参考文献

[1] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[J]. Advances in neural information processing systems, 2014, 27.

[2] Generative Models

[2] PyTorch 学习笔记（十）：初识生成对抗网络（GANs）

[3] 通俗理解生成对抗网络GAN

目录