推荐系统——DeepWalk算法

 搜索·推荐·广告   |  2020年09月16日   |  阅读：2064次

1. 概述

DeepWalk算法是在KDD2014中提出的算法，最初应用在图表示（Graph Embedding）方向，由于在推荐系统中，用户的行为数据固然的可以表示成图的形式，如下图所示：

在这里插入图片描述

通过Graph Embedding得到图中每个item的Embedding表示，DeepWalk算法常被用于推荐系统。Graph Embedding使用低维稠密向量的形式表示图中的节点，使得在原始图中相似（不同的方法对相似的定义不同）的节点其在低维表达空间也接近。

2. 算法思想

DeepWalk算法借鉴了word2vec算法的思想，word2vec是NLP中一种常用的word embedding方法，word2vec通过语料库中的句子序列来描述词与词的共现关系，进而学习到词语的向量表示。DeepWalk算法与word2vec类似，使用图中节点与节点的共现关系来学习节点的向量表示。在DeepWalk中通过使用随机游走(RandomWalk)的方式在图中进行节点采样来模拟语料库中的预料，进而使用word2vec的方式学习出节点的共现关系，其具体过程如下图所示：

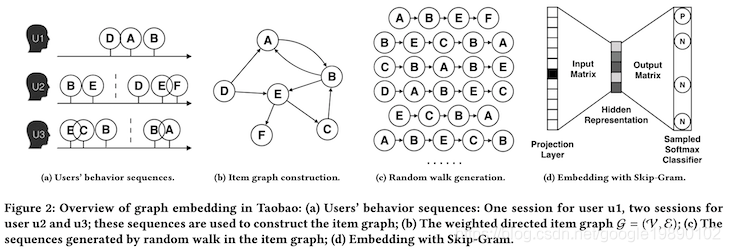
在这里插入图片描述

具体过程为：

  1. 抽取用户的行为序列，如图中(a)所示；
  2. 将用户的行为序列转换成图的表示方法，如图中(b)所示；
  3. 使用RandomWalk对图中节点采样，得到节点序列的表示，如图中©所示；
  4. 使用Skip-Gram学习出节点的Embedding表示，如图中(d)所示。

DeepWalk算法思想具体过程如下所示：

在这里插入图片描述

2.1. RandomWalk

RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点，从其邻居中随机采样节点作为下一个访问节点，重复此过程，直到访问序列长度满足预设条件。假设图为G=(V,E)G=\left ( V,E \right )，其中，VV表示图中点的集合，EE表示图中边的集合，在RandomWalk中关键的问题是如何计算从节点viv_i跳转到节点vjv_j的概率P(vj∣vi)P\left ( v_j\mid v_i \right )：

P(vj∣vi)={Mij∑j∈N+(vi)Mij if vi∈N+(vi)0 if eij∉EP\left ( v_j\mid v_i \right )=\begin{cases} \frac{M_{ij}}{\sum _{j\in N_+\left ( v_i \right )}M_{ij}} & \text{ if } v_i\in N_+\left ( v_i \right ) \\ 0 & \text{ if } e_{ij}\notin E \end{cases}

其中，EE是图中所有边的集合，N+(vi)N_+\left ( v_i \right )是节点viv_i所有的出边的集合，MijM_{ij}是节点viv_i到节点vjv_j的边的权重，对于无向无权图Mij=1M_{ij}=1。RandomWalk的代码大致如下：

def deep_worker(self):
	for _ in range(self.nums):
		for node in self.G.nodes():
			self.node_series.append(self.random_walker(node))
 
def random_walker(self, first_node):
	series = [first_node]
	for _ in range(1, self.walk_length):
		nodes_list = list(self.G.adj[first_node])
		first_node = random.choice(nodes_list)
		series.append(first_node)
	return series

2.2. word2vec

word2vec的基本原理不再在本文中详细给出，可以参阅其他的一些材料，Python下可以通过gensim里的Word2Vec实践：

from gensim.models import Word2Vec
w2v_model = Word2Vec(walks,sg=1,hs=1)

参考文献

[1] Perozzi B, Alrfou R, Skiena S. DeepWalk: online learning of social representations[J]. 2014:701-710.

[2] Wang J , Huang P , Zhao H , et al. Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba[J]. 2018.

[3] DeepWalk源码

[4] 《DeepWalk: Online Learning of Social Representations》笔记

[5] C实现的DeepWalk

目录