卷积神经网络AlexNet

 CV   |  2022年08月27日   |  阅读：1855次

1. 概述

AlexNet卷积神经网络[1]在CNN的发展过程中起着非常重要的作用，AlexNet是由加拿大多伦多大学的Alex Krizhevsky等人提出。在当年的ImageNet图像分类竞赛，取得了大赛的冠军并且效果大大好于第二名。如今回过来看，AlexNet的主要贡献是ReLU、Dropout、Max-Pooling，这些技术基本上在AlexNet之后的大多数主流架构中都能见到。

2. 算法的基本思想

2.1. AlexNet的网络结构

AlexNet的网络结构如下图所示：

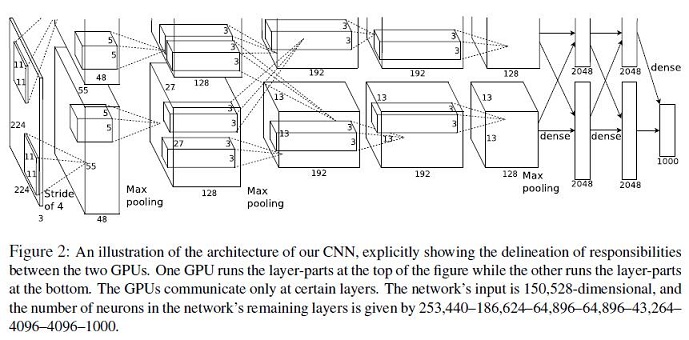
这里写图片描述

抛开两个GPU的结构不说，这主要是因为受当时的计算环境的影响。聚焦在AlexNet的结构，AlexNet网络中包含5个卷积层和3个全连接层。参照[2]的参数格式，可以绘制出如下的网络结构：

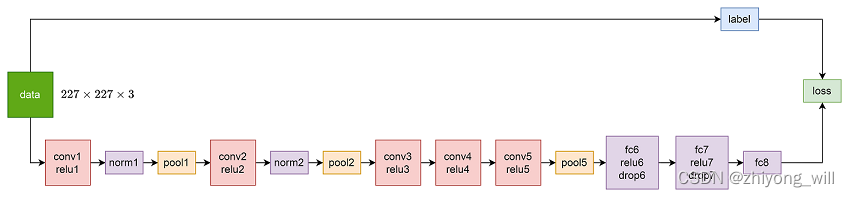
在这里插入图片描述

构建AlexNet也是通过不断堆叠各个模块，要理解各模块的作用，前提熟悉对各模块的输入输出维度。

  • data：大小为227×227×3227\times 227\times 3（此处参考文献[1]和[2]中的数值不一致，重在理解其原理）
  • conv1 & relu1
    • conv1：输入：227×227×3227\times 227\times 3
    • conv1：输出：55×55×9655\times 55 \times 96，其中，卷积核大小为11×1111\times 11，步长为44，根据公式(W−F+2P)/S+1\left ( W-F+2P \right )/S+1（其中，WW为输入大小，FF为卷积核大小，PP为padding大小，此处为00，S为步长），求解得到输出大小为5555
    • relu1：输入：55×55×9655\times 55 \times 96
    • relu1：输出：55×55×9655\times 55 \times 96
  • norm1：输入：55×55×9655\times 55 \times 96，输出：55×55×9655\times 55 \times 96
  • pool1：输入：55×55×9655\times 55 \times 96，输出：27×27×9627\times 27 \times 96，其中，卷积核大小为3×33\times 3，步长为22，根据上述公式，求解得到输出大小为2727
  • conv2 & relu2
    • conv2：输入：27×27×9627\times 27 \times 96
    • conv2：输出：27×27×25627\times 27 \times 256，其中，卷积核大小为5×55\times 5，步长为11，padding为22，最终的输出大小为2727
    • relu2：输入：27×27×25627\times 27 \times 256
    • relu2：输出：27×27×25627\times 27 \times 256
  • norm2：输入：27×27×25627\times 27 \times 256，输出：27×27×25627\times 27 \times 256
  • pool2：输入：27×27×25627\times 27 \times 256，输出：13×13×25613\times 13 \times 256，其中，卷积核大小为3×33\times 3，步长为22，根据上述公式，求解得到输出大小为1313
  • conv3 & relu3
    • conv3：输入：13×13×25613\times 13 \times 256
    • conv3：输出：13×13×38413\times 13 \times 384，其中，卷积核大小为3×33\times 3，步长为11，padding为11，最终的输出大小为1313
    • relu3：输入：13×13×38413\times 13 \times 384
    • relu3：输出：13×13×38413\times 13 \times 384
  • conv4 & relu4
    • conv4：输入：13×13×38413\times 13 \times 384
    • conv4：输出：13×13×38413\times 13 \times 384，其中，卷积核大小为3×33\times 3，步长为11，padding为11，最终的输出大小为1313
    • relu4：输入：13×13×38413\times 13 \times 384
    • relu4：输出：13×13×38413\times 13 \times 384
  • conv5 & relu5
    • conv5：输入：13×13×38413\times 13 \times 384
    • conv5：输出：13×13×25613\times 13 \times 256，其中，卷积核大小为3×33\times 3，步长为11，padding为11，最终的输出大小为2727
    • relu5：输入：13×13×25613\times 13 \times 256
    • relu5：输出：13×13×25613\times 13 \times 256
  • pool5：输入：13×13×25613\times 13 \times 256，输出：6×6×2566\times 6 \times 256，其中，卷积核大小为3×33\times 3，步长为22，根据上述公式，求解得到输出大小为66
  • fc6 & relu6 & drop6
    • fc6：输入：6×6×2566\times 6 \times 256，输出：40964096，通过对输入数据flatting，得到92169216维的数据
    • relu6：输入：40964096，输出：40964096
  • fc7 & relu7 & drop7
    • fc6：输入：40964096，输出：40964096
    • relu6：输入：40964096，输出：40964096
  • fc8：输入40964096，输出：10001000

2.2. 卷积过程

上面通过数据的输入到输出维度的变化对AlexNet的结构做了详细的描述，那么conv1中，数据是如何从227×227×3227\times 227\times 3到55×55×9655\times 55 \times 96的转换的，同时，参数的个数是多少？

参考文献[3]给出了具体的计算过程，输入的维度为5×5×35\times 5\times 3，卷积核的大小为3×3×33\times 3\times 3，卷积核的个数为22，padding为11，则最终的输出维度为3×3×23\times 3\times 2。其具体的计算过程如下图（在参考文献[3]的图上增加了标记）所示：

在这里插入图片描述

最终的输出的计算方法为：

o0=x0w00+x1w01+x2w02+b0o_0=x_0w0_0+x1w0_1+x2w0_2+b0

对于一个卷积核，其参数个数为3×3×3+13\times 3\times 3 + 1，那么从227×227×3227\times 227\times 3到55×55×9655\times 55 \times 96的转换，需要的参数个数为(11×11×3+1(opt))×96\left ( 11\times 11\times 3 + 1\left ( opt \right ) \right )\times 96。

2.3. ReLU激活函数

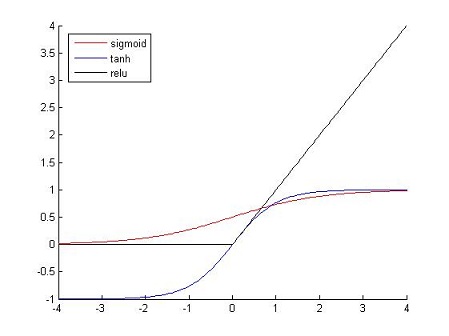
在神经网络中，使用的激活函数通常有：Sigmoid函数，Tanh函数。这两个激活函数属于饱和非线性（saturating nonlinearities），在训练的过程中会出现梯度弥散的现象（反向传播时梯度接近为0），在梯度下降法过程中比非饱和非线性的激活函数的训练速度慢，而Rectified Linear Units（ReLUs） 。

ReLU激活函数的具体形式为：

f(x)=max(0,x)f\left ( x \right )=max\left ( 0,x \right )

其函数的图像如下图所示：

这里写图片描述

2.4. Dropout

在AlexNet中，提出使用Dropout[3]避免模型的过拟合。Dropout策略是在模型的训练过程中，网络以概率1−p1-p随机丢弃一些神经元，如下图所示：

在这里插入图片描述

模型训练后，在进行测试时，不再使用Dropout丢弃神经元，而是将每个权重值乘上保留概率pp，表示他们对最后的预测结果的平均贡献，以达到与在训练时使用Dropout相同的效果，具体过程如下图所示：

在这里插入图片描述

Q：为什么Dropout通常应用在全连接层？
A：在卷积层中，由于卷积和ReLU激活函数引入的稀疏化等原因，Dropout策略在卷积层中使用较少。Dropout是用来防止网络模型的过拟合，而当模型过于复杂（即网络参数过多）才会容易过拟合，因此在卷积层中没必要。

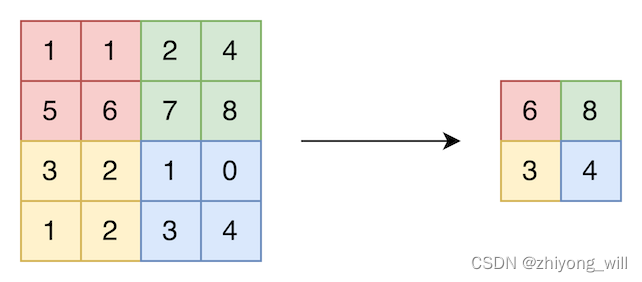
2.5. Max-Pooling

Max-Pooling是指在核的大小覆盖区域内做max的操作，如下图所示，原始的输入大小为4×44\times 4，核的大小为2×22\times 2，步长为22，则最终的输出大小为2×22\times 2。以左上的红色区域为例，Max-Pooling在1,1,5,61,1,5,6中选择最大的值作为最终的输出。

在这里插入图片描述

2.6. 输入图像的处理

对于一个任意大小的图片来说，要想输入到CNN网络中，需要对图像的大小做处理，使得其图像具有固定的维度，如上述的227×227×3227\times 227\times 3，但通常一开始会将图片处理成256×256×3256\times 256\times 3。首先需要按照短边缩放到256256，再根据中心裁剪出256×256256\times 256的大小，其具体过程如下图所示：

在这里插入图片描述

至于256×256×3256\times 256\times 3到227×227×3227\times 227\times 3，可以通过多次的裁剪生成多组训练数据，这也能起到一定的数据增强作用。对于输入到模型中的数据，每个像素点需要减去训练数据在该维度上的均值。

2.7. Local Response Normalization

局部响应归一化LRN（Local Response Normalization）是一种增强模型泛化能力的方法，在LRN中，通过对局部神经元的活动创建竞争机制，使其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，其具体公式如下所示：

bx,yi=ax,yi/(k+α∑j=max(0,i−n/2)min(N−1,i+n/2)(ax,yj)2)βb_{x,y}^i=a_{x,y}^i/\left ( k+\alpha \sum_{j=max\left ( 0,i-n/2 \right )}^{min\left ( N-1,i+n/2 \right )}\left ( a_{x,y}^j \right )^2 \right )^\beta

其中，ax,yia_{x,y}^i表示卷积核ii在坐标(x,y)\left ( x,y\right)处的神经元激活值，bx,yib_{x,y}^i表示归一化后的激活值。

3. 总结

AlexNet网络的提出是在传统机器学习方法向深度学习转变的时期，通过在ImageNet图像分类竞赛中的优秀表现，也证实了卷积神经网络在图像领域的优秀表现，同时在AlexNet中提出的方法在后续的网络中一直被沿用，如ReLU、Dropout、Max-Pooling。通过对AlexNet网络的分析，我们发现对于一个深度卷积神经网络，通常应该具备如下的模块：

  • 卷积模块
  • Pooling模块
  • 激活函数
  • 归一化

然而在后续的CNN中，局部响应归一化LRN并未得到延续。

参考文章

[1] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Advances in neural information processing systems, 2012, 25.

[2] http://dgschwend.github.io/netscope/#/preset/alexnet

[3] https://cs231n.github.io/convolutional-networks/

[3] Srivastava N , Hinton G , Krizhevsky A , et al. Dropout: A Simple Way to Prevent Neural Networks from Overfitting[J]. Journal of Machine Learning Research, 2014, 15(1):1929-1958.

[4] 对dropout的理解详细版

目录