1. 概述

GAN的出现为数据生成提供了一种新的思路，以图像生成为例，在GAN框架中，不再需要其他复杂的操作，如Markov Chain等，只需要对定义好的网络进行backpropagation即可完成生成网络的训练。在原始的GAN框架中，包括了两个部分，分别为生成网络（Generator）$G$和判别网络（Discriminator）$D$，其中生成网络（Generator）$G$用于生成图片，判别网络（Discriminator）$D$用于判别一张图片是否是真实的。通过不断提高生成网络$G$的生成质量，最终“骗”过判别网络$D$，在此过程中，判别网络$D$也在不断提高自身的判别能力，通过如此的一个动态的“博弈”过程，最终，训练好的生成网络$G$便可以用于生成“以假乱真”的图片。

然而在所有的过程中，无论是生成过程还是判别过程都是无任何指导的，Conditional GAN[1]提出在上述的两个过程中引入一个条件，以此指导上述的两个过程。

2. 算法原理

2.1. GAN原理回顾

在原始的GAN框架中，包括了两个部分，分别为生成网络（Generator）$G$和判别网络（Discriminator）$D$，其中：

• 生成网络（Generator）$G$用于生成图片，其输入是一个随机的噪声$\boldsymbol{z}$，通过这个噪声生成图片，记作$G\left ( \boldsymbol{z} \right )$
• 判别网络（Discriminator）$D$用于判别一张图片是否是真实的，对应的，其输入是一整图片$\boldsymbol{x}$，输出$D\left ( \boldsymbol{x} \right )$表示的是图片$\boldsymbol{x}$为真实图片的概率

在GAN框架的训练过程中，希望生成网络$G$生成的图片尽量真实，能够欺骗过判别网络$D$；而对于判别网络$D$，希望能够把$G$生成的图片从真实图片中区分开。这样的一个过程就构成了一个动态的“博弈”。最终，GAN希望能够使得训练好的生成网络$G$生成的图片能够以假乱真，即对于判别网络$D$来说，无法判断$G$生成的网络是不是真实的。此时，训练好的生成网络$G$便可以用于生成“以假乱真”的图片。

GAN的价值函数：

$$\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )=\mathbb{E}_{\boldsymbol{x}\sim p_{data}\left ( \boldsymbol{x} \right )}\left [ log\; D\left ( \boldsymbol{x} \right ) \right ]+\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}\left ( \boldsymbol{z} \right )}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z} \right ) \right ) \right ) \right ]$$

GAN的训练过程如下所示：

2.2. Conditional GAN

Conditional GAN的思想也比较简单，在GAN的基础上增加了条件输入，在生成网络和判别网络中分别加入一个条件输入$\boldsymbol{y}$，$\boldsymbol{y}$可以为任何的额外信息，分别与原始的$\boldsymbol{x}$和$\boldsymbol{z}$这两个输入concat在一起，如下图所示：

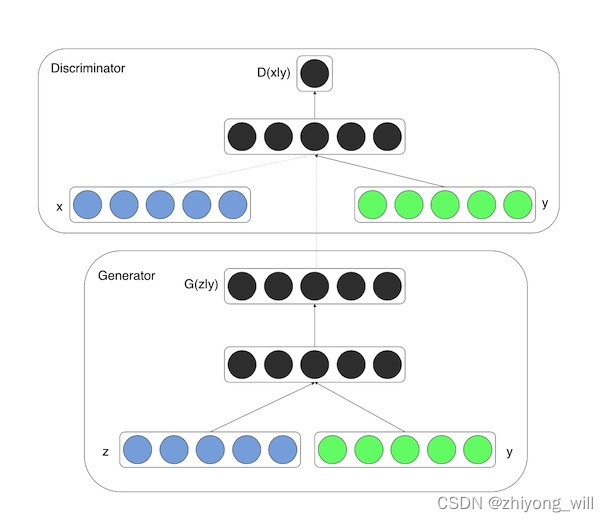
Conditional GAN的价值函数：

$$\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )=\mathbb{E}_{\boldsymbol{x}\sim p_{data}\left ( \boldsymbol{x} \right )}\left [ log\; D\left ( \boldsymbol{x}\mid \boldsymbol{y} \right ) \right ]+\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}\left ( \boldsymbol{z} \right )}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}\mid \boldsymbol{y} \right ) \right ) \right ) \right ]$$

假设从真实数据中采样$m$个样本$\left \{ \boldsymbol{x}^{\left ( 1 \right )},\boldsymbol{x}^{\left ( 2 \right )},\cdots ,\boldsymbol{x}^{\left ( m \right )} \right \}$，从噪音分布$p_g\left ( \boldsymbol{z} \right )$中同样采样$m$个样本，记为$\left \{ \boldsymbol{z}^{\left ( 1 \right )},\boldsymbol{z}^{\left ( 2 \right )},\cdots ,\boldsymbol{z}^{\left ( m \right )} \right \}$，针对每一个样本，都有一个对应的条件，记为$\left \{ \boldsymbol{y}^{\left ( 1 \right )},\boldsymbol{y}^{\left ( 2 \right )},\cdots ,\boldsymbol{y}^{\left ( m \right )} \right \}$，此时，上述价值函数可以近似表示为：

$$\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )\approx \sum_{i=1}^{m}\left [ log\; D\left ( \boldsymbol{x}^{\left ( i \right )}\mid \boldsymbol{y}^{\left ( i \right )} \right ) \right ]+\sum_{i=1}^{m}\left [ log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )}\mid \boldsymbol{y}^{\left ( i \right )} \right ) \right ) \right ) \right ]$$

简化后为：

$$\underset{G}{min}\; \underset{D}{max}\; V\left ( D,G \right )\approx \sum_{i=1}^{m}\left [ log\; D\left ( \boldsymbol{x}^{\left ( i \right )}\mid \boldsymbol{y}^{\left ( i \right )} \right ) + log\; \left ( 1-D\left ( G\left ( \boldsymbol{z}^{\left ( i \right )}\mid \boldsymbol{y}^{\left ( i \right )} \right ) \right ) \right ) \right ]$$

训练过程中只需修改上述的梯度公式，其余与GAN的训练一致。

3. 总结

Conditional GAN的思路相对于传统的GAN来说比较直接，在生成网络和判别网络的输入中增加一些额外的信息，用于指导整个过程的训练。

参考文献

[1] Mirza M, Osindero S. Conditional generative adversarial nets[J]. arXiv preprint arXiv:1411.1784, 2014.