1. 概述

相比较于基于Collaborative Filter算法，基于基础Graph Embedding模型可以根据用户的行为序列学习出item的embedding，利用item对应的Embedding可以方便计算item与item之间的相似度，并在实践中被证明是卓有成效的方法，在基于基础Graph Embedding模型，主要包括item2vec，node2vec，deepwalk等算法。

在使用基础Graph Embedding算法的前提是用户的行为序列，但是对于一些新的item或者用户很少有行为的item，即冷启动问题，基础的Graph Embedding算法很难学到对应item的embedding表示，为此，一些针对item冷启动的方法被提出，其中就包括GES和EGES算法。

GES和EGES是阿里在2018年提出的两个基于Graph Embedding的算法，其中GES全称为Graph Embedding with Side Information，EGES全称为Enhanced Graph Embedding with Side Information。为了解决冷启动的问题，GES和EGES在计算item embedding的过程中引入了side information。

2. 算法原理

2.1. side information

side information在推荐系统中有着重要的作用，不仅仅能应用在召回中用于处理冷启动问题，同时在排序阶段中也有广泛的应用。side information主要指的是与item相关的一些先验信息，对于商品而言，先验信息包括：类别，商店，价格等。

2.2. GES算法

GES算法全称为Graph Embedding with Side Information，假设$\mathbf{W}$表示item或者side information的embedding矩阵，其中，$\mathbf{W}_v^0$表示item $v$的embedding，$\mathbf{W}_v^s$表示第$s$个side information，item $v$共有$n$个side information，则对于item $v$共有$n+1$个向量：

$$\mathbf{W}_v^0，\cdots ,\mathbf{W}_v^n\in \mathbb{R}^d$$

其中，$d$为embedding的维度。

对于item $v$，使用average-pooling将这$n+1$个向量聚合起来，得到item $v$的向量表示：

$$\mathbf{H}_v=\frac{1}{n+1}\sum_{s=0}^{n}\mathbf{W}_v^s$$

2.3. EGES算法

EGES算法全称为Enhanced Graph Embedding with Side Information，从其名字来看便可以知道，EGES是GES的增强版。在GES中，每一个向量，包括一个item的向量以及$n$个side information的向量，这些向量的权重是一样的。从实际的情况来看，不同种类的side information对于最终的embedding的贡献是不一样的。因此EGES对GES中的向量做了加权的操作。

假设对于item $v$，权重矩阵为$\mathbf{A}\in\mathbb{R}^{\left | V \right |\times \left ( n+1 \right )}$，其中，$\mathbf{A}_{ij}$表示第$i$个item的第$j$个side information的权重，为简单，记$a_i^j$为$\mathbf{A}_{ij}$，$\mathbf{A}_{i0}$表示的是item $i$本身向量的权重，记为$a_i^0$。

对于item $v$，加权平均后的结果为：

$$\mathbf{H}_v=\frac{\sum _{j=0}^ne^{a_v^j}\mathbf{W}_v^j}{\sum _{j=0}^ne^{a_v^j}}$$

其中，使用$e^{a_v^j}$而不是$a_v^j$是为了保证权重大于0。

2.4. GES和EGES的模型结构

GES和EGES的模型结构如下图所示：

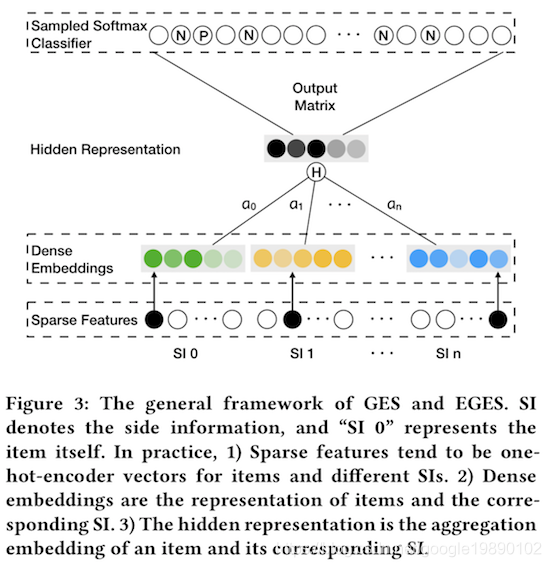
其中，Dense Embeddings表示的是item向量以及$n$个side information的向量。Hidden Representation即为如上公式中的$\mathbf{H}_v$。从上述过程来看，GES即为EGES模型的简化版本，即权重都为$\frac{1}{n+1}$。

2.5. EGES中item向量的求解

EGES算法的流程如下图所示：

从EGES算法的流程中，笔者发现，其与DeepWalk的流程基本一致，不同的主要是两点：1）学习的参数不同，在DeepWalk中主要是item的向量表示，在EGES中不仅要学习item的向量$\mathbf{W}^0$，$n$个side information的向量$\mathbf{W}^1,\cdots \mathbf{W}^n$，还包括权重的矩阵$\mathbf{A}$；2）在DeepWalk中使用的是SkipGram，在EGES中使用的是WeightedSkipGram。

2.6. Weighted Skip-Gram

Weighted Skip-Gram算法的流程如下所示：

为了能够更好的理解上述的流程，我们需要先了解word2vec中Skip-Gram模型的具体流程，在词向量的求解过程中除了Skip-Gram还可以是CBOW模型，本文的重点是Skip-Gram模型，Skip-Gram模型的结构如下图所示：

为讨论的方便，假设在Skip-Gram模型中，每个词的向量维度为$d$，在词典$V$中，中心词$w_c$的词向量为$v_c\in \mathbb{R}^d$，背景词$w_o$的词向量为$u_o\in \mathbb{R}^d$。给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

$$P\left ( w_o\mid w_c \right )=\frac{exp\left ( u_o^Tv_c \right )}{\sum _{i\in V}exp\left ( u_i^Tv_c \right )}$$

此时，对于整个文本可以得到如下的概率形式：

$$\prod_{t=1}^{T}\prod _{-m\leqslant j\leqslant m,j\neq 0}P\left ( w^{\left ( t+j \right )}\mid w^{\left ( t \right )} \right )$$

语言模型中的目标是要使得上述的概率最大，通过log似然，可以得到如下的损失函数：

$$-\prod_{t=1}^{T}\prod _{-m\leqslant j\leqslant m,j\neq 0}log\; P\left ( w^{\left ( t+j \right )}\mid w^{\left ( t \right )} \right )$$

对于$log\; P\left ( w_o\mid w_c \right )$，有：

$$log\; P\left ( w_o\mid w_c \right )=u_o^Tv_c-log\left ( \sum _{i\in V}exp\left ( u_i^Tv_c \right ) \right )$$

为了能够对其中的参数求解，可以使用梯度下降法求解，此时需要对损失函数求导，以$\frac{\partial log\; P\left ( w_o\mid w_c \right )}{\partial v_c}$为例：

$$\frac{\partial log\; P\left ( w_o\mid w_c \right )}{\partial v_c}=u_o-\sum _{j\in V}P\left ( w_j\mid w_c \right )\cdot u_j$$

从上述的公式发现，每次的求导数的过程中，都需要对整个词典中的词计算，如果词典较大，那么每次更新时的计算成本就比较大，为降低计算成本，近似的训练方法被提出，负采样（Negative Sampling）便是其中的一种近似计算方法。

对于上述给定的中心词$w_c$，给定一个背景窗口，假设背景词$w_o$出现在$w_c$的背景窗口中的事件概率为：

$$P\left ( D=1\mid w_c,w_o \right )=\sigma \left ( u_o^Tv_c \right )$$

对于给定的长度为$T$的文本，假设时间步$t$的词为$w^{\left ( t \right )}$且背景窗口大小为$m$，此时联合概率为：

$$\prod_{t=1}^{T}\prod _{-m\leqslant j\leqslant m,j\neq 0}P\left ( D=1\mid w^{\left ( t \right )},w^{\left ( t+j \right )} \right )$$

此时模型中仅考虑了正样本，通过采样$K$个未出现在该背景窗口中的词，此时的联合概率为：

$$\prod_{t=1}^{T}\prod _{-m\leqslant j\leqslant m,j\neq 0}P\left ( w^{\left ( t+j \right )}\mid w^{\left ( t \right )} \right )$$

其中，$P\left ( w^{\left ( t+j \right )}\mid w^{\left ( t \right )} \right )$可以表示为：

$$P\left ( w^{\left ( t+j \right )}\mid w^{\left ( t \right )} \right )=P\left ( D=1\mid w^{\left ( t \right )},w^{\left ( t+j \right )} \right )\cdot \prod_{k=1}^{K}P\left ( D=0\mid w^{\left ( t \right )},w_k \right )$$

可以验证，此时计算不再与词典大小相关，而是与负采样的参数$K$相关，以上便是Skip-Gram模型以及负采样的相关内容。

对于采样到的样本$u$，其对应的向量为$\mathbf{Z}_u$，由上述的理论可以得到：

$$\mathfrak{L}\left ( v,u,y \right )=-\left [ ylog\left ( \sigma \left ( \mathbf{H}_v^T\mathbf{Z}_u \right ) \right )+\left ( 1-y \right )log\left ( 1-\sigma \left ( \mathbf{H}_v^T\mathbf{Z}_u \right ) \right ) \right ]$$

可以得到如下的导数：

$$\frac{\partial \mathfrak{L}}{\partial \mathbf{Z}_u}=\left ( \sigma \left ( \mathbf{H}_v^T\mathbf{Z}_u \right )-y \right )\mathbf{H}_v$$

$$\frac{\partial \mathfrak{L}}{\partial a_v^s}=\left ( \sigma \left ( \mathbf{H}_v^T\mathbf{Z}_u \right )-y \right )\mathbf{Z}_u\frac{\left ( \sum_{j=0}^{n}e^{a_v^j} \right )e^{a_v^s}\mathbf{W}_v^s-e^{a_v^s}\sum_{j=0}^{n}e^{a_v^j}\mathbf{W}_v^j}{\left ( \sum_{j=0}^{n}e^{a_v^j} \right )^2}$$

$$\frac{\partial \mathfrak{L}}{\partial \mathbf{W}_v^s}=\frac{e^{a_v^s}}{\sum_{j=0}^{n}e^{a_v^j}}\left ( \sigma \left ( \mathbf{H}_v^T\mathbf{Z}_u \right )-y \right )\mathbf{Z}_u$$

参考文献

[1] Wang J, Huang P, Zhao H, et al. Billion-scale commodity embedding for e-commerce recommendation in alibaba[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 839-848.

[2] [Graph Embedding]阿里超大规模商品Embedding策略EGES

[3] Graph Embedding在淘宝推荐系统中的应用

[4] NLP之—word2vec算法skip-gram原理详解