长短期记忆网络LSTM

 NLP   |  2020年09月20日   |  阅读：693次

1. 概述

在循环神经网络RNN一文中提及到了循环神经网络RNN存在长距离依赖的问题，长短期记忆（Long Short-Term Memory，LSTM）网络便是为了解决RNN中存在的梯度爆炸的问题而提出。在LSTM网络中，主要依靠引入“门”机制来控制信息的传播。

2. 算法原理

2.1. LSTM的网络结构

LSTM的网络结构如下所示（图片来自参考文献）：

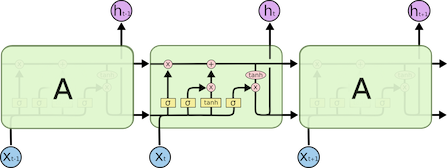
在这里插入图片描述

与循环神经网络RNN相比，LSTM的网络结构要复杂的多。

在LSTM网络中，通过引入三个门来控制信息的传递，这三个门分别为遗忘门（forget gate），输入门（input gate）和输出门（output gate）。门机制是LSTM中重要的概念，那么什么是“门”以及门机制在LSTM中是如何解决长距离依赖的问题的。

2.2. 门机制

现实中的“门”通常解释为出入口，在LSTM网络的门也是一种出入口，但是是控制信息的出入口。门的状态通常有三种状态，分别为全开（信息通过概率为1），全闭（信息通过概率为0）以及半开（信息通过概率介于0和1之间）。在这里，我们发现对于全开，全闭以及半开三种状态下的信息通过可以通过概率来表示，在神经网络中，sigmoid函数也是一个介于0和1之间的表示，可以应用到LSTM中门的计算中。

2.3. LSTM的计算过程

如下是LSTM的网络结构的具体形态，如下所示（图片来自邱锡鹏老师的课件）：

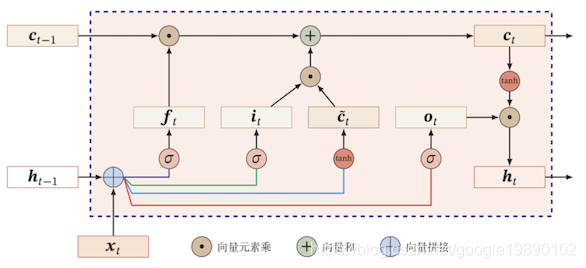
在这里插入图片描述

其中，ct−1c_{t-1}表示的是t−1t-1时刻的cell state（注：关于cell state，查了多个版本的中文翻译，有翻译为“细胞状态”，有翻译成“单元状态”，邱老师使用的是内部状态，没有一个明确的中文翻译，故在此使用英文），ht−1h_{t-1}表示的是t−1t-1时刻的hidden state（注：与前面的cell state对应），xtx_t表示的是tt时刻的输入，ftf_t表示的是遗忘门，iti_t表示的是输入门，c~t\tilde{c}_t表示的是候选值（candidate values），oto_t表示的是输出门。

从图中的数据流向得到的计算流程如下所示：

  1. 利用t−1t-1时刻的hidden state ht−1h_{t-1}计算遗忘门ftf_t的结果，ftf_t的计算公式如下所示

ft=σ(Wfxt+Ufht−1+bf)f_t=\sigma \left ( W_fx_t+U_fh_{t-1}+b_f \right )

  1. 利用t−1t-1时刻的hidden state ht−1h_{t-1}计算输入门iti_t的结果，iti_t的计算公式如下所示

it=σ(Wixt+Uiht−1+bi)i_t=\sigma \left ( W_ix_t+U_ih_{t-1}+b_i \right )

  1. 利用t−1t-1时刻的hidden state ht−1h_{t-1}计算候选值c~t\tilde{c}_t的结果，c~t\tilde{c}_t的计算公式如下所示

c~t=tanh(Wcxt+Ucht−1+bc)\tilde{c}_t=tanh \left ( W_cx_t+U_ch_{t-1}+b_c \right )

  1. 利用t−1t-1时刻的hidden state ht−1h_{t-1}计算输出门oto_t的结果，oto_t的计算公式如下所示

ot=σ(Woxt+Uoht−1+bo)o_t=\sigma \left ( W_ox_t+U_oh_{t-1}+b_o \right )

  1. 根据tt时刻的cell state ctc_t，这里会使用到t−1t-1时刻的cell state ct−1c_{t-1}，遗忘门ftf_t，输入门iti_t和候选值c~t\tilde{c}_t，ctc_t的计算公式如下所示

ct=ft⊙ct−1+it⊙c~tc_t=f_t\odot c_{t-1}+i_t\odot \tilde{c}_t

上述的公式是由前面的1，2，3部分的公式组成，也是LSTM网络中的关键的部分，对该公式，我们从如下的几个部分来理解：

  • ft⊙ct−1f_t\odot c_{t-1}，使用遗忘门ftf_t对t−1t-1时刻下的cell state ct−1c_{t-1}遗忘；
  • it⊙c~ti_t\odot \tilde{c}_t，首先是c~t\tilde{c}_t表示的是通过tt时刻的输入和t−1t-1时刻的hidden state ht−1h_{t-1}需要增加的信息，与输入门iti_t结合起来就表示整体需要增加的信息；
  • 两部分结合表示的是tt时刻下的cell state下需要从t−1t-1时刻下的cell state中保留的部分信息以及tt时刻下新增信息的总和。
  1. 根据输出门oto_t和cell state ctc_t计算外部状态hth_t，hth_t的计算公式如下所示

ht=ot⊙tanh(ct)h_t=o_t\odot tanh\left ( c_t \right )

参考文献

[1] Understanding LSTM Networks

[2] LSTM与GRU的原理，不熟悉的再来看看呀

[3] 神经网络与深度学习

[4] 人人都能看懂的LSTM